ASTM E2246-02

NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: E 2246 – 02
Standard Test Method for
Strain Gradient Measurements of Thin, Reflecting Films
Using an Optical Interferometer
This standard is issued under the fixed designation E2246; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (e) indicates an editorial change since the last revision or reapproval.
1. Scope 3.1.3 anchor, n—in a surface-micromachining process, the
portion of the test structure where the mechanical layer makes
1.1 This test method covers a procedure for measuring the
contact with the underlying layer (see Figs. 1 and 2).
strain gradient in thin, reflecting films. It applies only to films,
3.1.4 anchor lip, n—in a surface-micromachining process,
such as found in microelectromechanical systems (MEMS)
the extension of the mechanical layer around the edges of the
materials, which can be imaged using an interferometer.
anchor (see Figs. 2 and 3).
Measurements from cantilevers that are touching the underly-
3.1.5 bulk micromachining, adj—a MEMS fabrication pro-
ing layer are not accepted.
cess where the substrate is removed at specified locations,
1.2 This test method uses a non-contact optical interferom-
which can create structures suspended in air.
eter with the capability of obtaining topographical 3-D data
3.1.6 cantilever, n—a test structure that consists of a beam
sets. It is performed in the laboratory.
suspended in air and anchored or supported at one end (see
1.3 This standard does not purport to address all of the
Figs. 1-3, and Fig. X1.1).
safety concerns, if any, associated with its use. It is the
3.1.7 fixed-fixed beam, n—a test structure that consists of a
responsibility of the user of this standard to establish appro-
beamsuspendedinairandanchoredorsupportedatbothends.
priate safety and health practices and determine the applica-
3.1.8 in-plane length measurement, n—a length (or deflec-
bility of regulatory limitations prior to use.
tion)measurementmadeparalleltotheunderlyinglayer(orthe
2. Referenced Documents
xy-plane).
3.1.9 interferometer, n—a non-contact optical instrument
2.1 ASTM Standards:
(suchasshowninFig.4)usedtoobtaintopographical3-Ddata
E2244 Test Method for In-Plane Length Measurements of
sets.
Thin, Reflecting Films Using an Optical Interferometer
3.1.10 mechanical layer, n—in a surface-micromachining
E2245 Test Method for Residual Strain Measurements of
process, the patterned layer (as shown in Fig. 2) that is
Thin, Reflecting Films Using an Optical Interferometer
anchoredtotheunderlyinglayerwherecutsaredesignedinthe
3. Terminology
sacrificial layer and that is suspended in air where no cuts are
designed in the sacrificial layer.
3.1 Definitions:
3.1.11 MEMS, adj—microelectromechanical systems.
3.1.1 2-D data trace, n—a two-dimensional data trace that
3.1.12 out-of-plane, adj—perpendicular (in the z-direction)
is extracted from a topographical 3-D data set and that is
to the underlying layer.
parallel to the xz-or yz-plane of the interferometer.
3.1.13 out-of-plane measurements, n—measurements taken
3.1.1.1 Discussion—The height of the sample is measured
on structures that are curved out-of-plane in the z-direction.
along the z-axis of the interferometer. The interferometer’s
3.1.14 residual strain, n—inasurface-micromachiningpro-
x-axis (as shown in Figs. 1-3) is typically aligned parallel or
cess,thestrainpresentinthemechanicallayerafterfabrication
perpendicular to the transitional edges to be measured.
yet before the sacrificial layer is removed. In a bulk-
3.1.2 3-D data set, n—a three-dimensional data set with a
micromachining process, the strain present in the suspended
topographical z-data value for each (x, y) pixel location within
layer after fabrication yet before the substrate is removed at
the interferometer’s field of view.
specified locations.
3.1.15 sacrificial layer, n—in a surface-micromachining
This test method is under the jurisdiction ofASTM Committee E08 on Fatigue
process, the layer fabricated between the mechanical layer and
and Fracture and is the direct responsibility of Subcommittee E08.05 on Cyclic
the underlying layer.This layer is removed after fabrication. If
Deformation and Fatigue Crack Formation.
cuts are designed in this sacrificial layer (as shown in Fig. 2),
Current edition approved Oct. 10, 2002. Published October 2002.
Annual Book of ASTM Standards, Vol 03.01.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, United States.
E2246–02
FIG. 1 Three-Dimensional View of Surface-micromachined Cantilever
NOTE 1—The underlying layer is beneath the entire test structure.
NOTE 2—The mechanical layer is included in both the light and dark gray areas.
NOTE 3—The dark gray area (the anchor) is the designed cut in the sacrificial layer. This is where the mechanical layer contacts the underlying layer.
NOTE 4—The light gray area is suspended in air after fabrication.
FIG. 2 Design Dimensions for Cantilever in Fig. 1
an anchor is created allowing the mechanical layer to contact 3.1.18 substrate, n—the thick, starting material in a MEMS
the underlying layer in that region. fabrication process.
3.1.16 stiction, n—in a surface-micromachining process, a 3.1.19 support region, n—in a bulk-micromachining pro-
structure exhibits this when a non-anchored portion of the cess, the region that marks the end of the suspended structure.
mechanical layer adheres to the top of the underlying layer. This region is suspended in air, attached to the substrate, or
3.1.17 strain gradient, n—the positive difference in the both.
strainbetweenthetopandbottomofacantileverdividedbyits 3.1.20 surface micromachining, adj—a MEMS fabrication
thickness. process where thin, sacrificial layers are removed, which can
3.1.17.1 Discussion—Consider a surface-micromachining create structures suspended in air.
process. The strain gradient is present in the cantilever before 3.1.21 test structure, n—a structure (such as, a cantilever or
the sacrificial layer is removed. After the sacrificial layer is afixed-fixedbeam)thatisusedtoextractinformation(suchas,
removed,thecantileverbowsout-of-planeintheplusorminus the strain gradient or the residual strain of a layer) about a
z-direction (as shown in Fig. 1). The strain gradient in this fabrication process.
cantilever is zero. Examining the out-of-plane measurements 3.1.22 transitional edge, n—an edge of a MEMS structure
ofthecantileverafterthesacrificiallayerisremovedallowsfor (such as Edge “1” in Fig. 3) that is characterized by a
the calculation of the strain gradient present in the cantilever distinctiveout-of-planeverticaldisplacement(asshowninFig.
before the sacrificial layer is removed. 5).
E2246–02
NOTE 1—The 2-D data traces (“a” and “e”) are used to ensure alignment.
NOTE 2—Trace “c” is used to determine the strain gradient and ascertain if the cantilever is adhered to the top of the underlying layer.
NOTE 3—Traces “b,” “c,” and “d” are used in the calculation of u .
W
FIG. 3 Top View of Surface-micromachined Cantilever
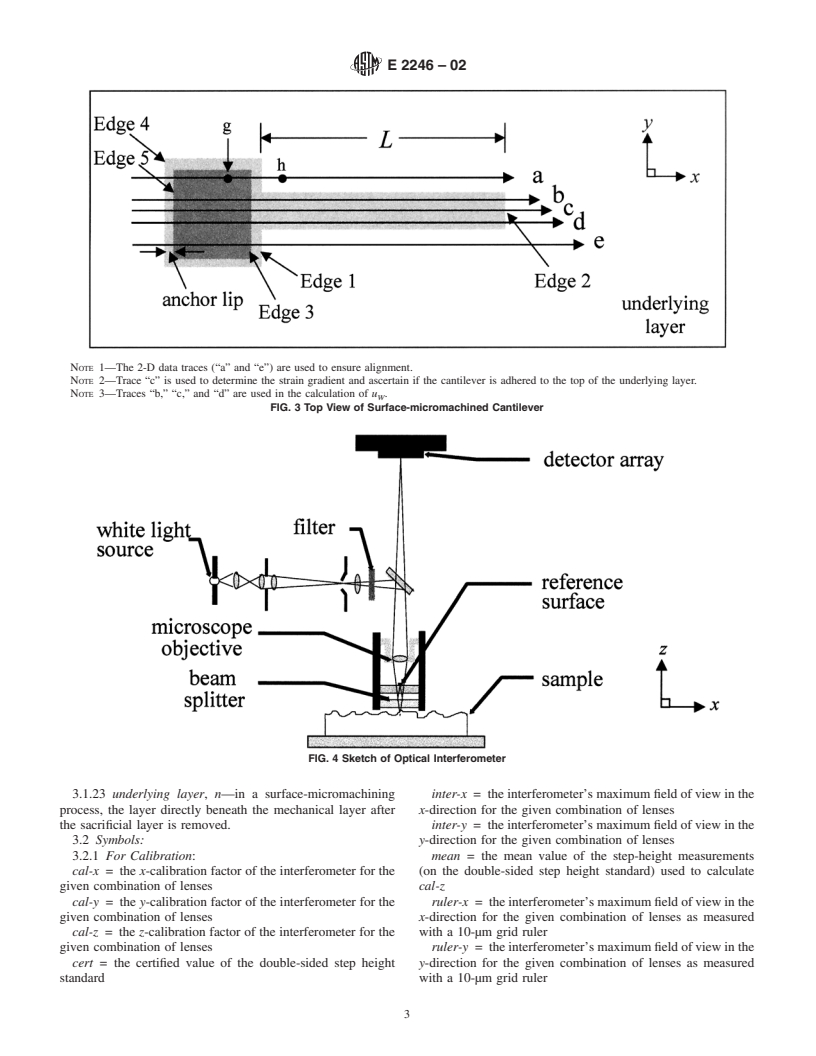
FIG. 4 Sketch of Optical Interferometer
3.1.23 underlying layer, n—in a surface-micromachining inter-x = theinterferometer’smaximumfieldofviewinthe
process, the layer directly beneath the mechanical layer after x-direction for the given combination of lenses
the sacrificial layer is removed. inter-y = theinterferometer’smaximumfieldofviewinthe
3.2 Symbols: y-direction for the given combination of lenses
3.2.1 For Calibration: mean = the mean value of the step-height measurements
cal-x = the x-calibration factor of the interferometer for the (on the double-sided step height standard) used to calculate
given combination of lenses cal-z
cal-y = the y-calibration factor of the interferometer for the ruler-x = theinterferometer’smaximumfieldofviewinthe
given combination of lenses x-direction for the given combination of lenses as measured
cal-z = the z-calibration factor of the interferometer for the with a 10-µm grid ruler
given combination of lenses ruler-y = theinterferometer’smaximumfieldofviewinthe
cert = the certified value of the double-sided step height y-direction for the given combination of lenses as measured
standard with a 10-µm grid ruler
E2246–02
FIG. 5 2-D Data Trace Used to Find x1 , x1 , x4 , and x4
lower upper lower upper
3.2.2 For Alignment: s = thestraingradient.Threedatapoints(suchasshownin
g
L = the in-plane length measurement of the cantilever (see Fig. 6) are used for this calculation
Fig. 2 or Fig. 3)
s = thestraingradientwhentheresidualstrainequalszero
g0
x1 = the x-datavaluealongEdge“1”(suchasshownin t = the thickness of the suspended layer, such as shown in
lower
Fig. 5) locating the lower part of the transition
Fig. X2.1 (2-4) for a surface-micromachining process
x1 = the x-datavaluealongEdge“1”(suchasshownin
t = in a bulk-micromachining process, the thickness
upper
support
Fig. 5) locating the upper part of the transition
of the support region where it is intersected by the 2-D data
x3 = the x-datavaluealongEdge“3”(suchasshownin
trace of interest (such as, Trace “a” or “e” in Fig. X1.1, as
lower
Fig. X1.2) locating the lower part of the transition
shown in Fig. X1.2)
x3 = the x-datavaluealongEdge“3”(suchasshownin
x1 = the average of x1 and x1
upper
ave lower upper
Fig. X1.2) locating the upper part of the transition
x2 = the average of x2 and x2
ave lower upper
x4 = the x-datavaluealongEdge“4”(suchasshownin
x2 = the x-data value along Edge “2” (as shown in Fig.
lower
lower
Fig. 5) locating the lower part of the transition
6) locating the lower part of the transition
x4 = the x-datavaluealongEdge“4”(suchasshownin
upper x2 = the x-data value along Edge “2” (as shown in Fig.
upper
Fig. 5) locating the upper part of the transition
6) locating the upper part of the transition
x = the x-data value along the transitional edge of
lower z = the z-data value associated with x
upper upper
interest locating the lower part of the transition (see Fig. 5)
z = in a bulk-micromachining process, the value for z
upper-t
x = the x-data value along the transitional edge of
upper when the thickness of the support region, t , is subtracted
support
interest locating the upper part of the transition (see Fig. 5)
from z
upper
3.2.3 For Strain Gradient Calculations:
3.2.4 For Combined Standard Uncertainty Calculations:
a = the x- (or y-) coordinate of the origin of the circle of
s = in determining the combined standard uncertainty
g-high
radius R . This circle models the out-of-plane shape in the
int
valueforthestraingradientmeasurement,thehighestvaluefor
z-direction of the topmost surface of the cantilever
s given the specified variations
g
b = the z-coordinateoftheoriginofthecircleofradius R .
int
s = in determining the combined standard uncertainty
g-low
This circle models the out-of-plane shape in the z-direction of
value for the strain gradient measurement, the lowest value for
the topmost surface of the cantilever
s given the specified variations
g
R = the radius of the circle modeling the shape of the
int
u = the component in the combined standard uncertainty
1pt
topmost surface of the cantilever as measured with the inter-
calculation that is due to the measurement uncertainty of one
ferometer (1)
data point
s = equals 1 for cantilevers deflected in the minus
u = the combined standard uncertainty value (that is, the
c
z-direction, and equals −1 for cantilevers deflected in the plus
estimated standard deviation of the result) (5).
z-direction
u = the component in the combined standard uncertainty
W
calculation that is due to the measurement uncertainty across
the width of the cantilever.
3 w = the half width of the interval from s to s
Theboldfacenumbersinparenthesesrefertothelistofreferencesattheendof 1/2 g-low g-high
this standard. 3.2.5 For Adherence to the Top of the Underlying Layer:
E2246–02
FIG. 6 2-D Data Trace Used to Find x2 , x2 , and the Three Data Points
lower upper
A = the minimum thickness of the mechanical layer as 4.2 Toobtainthreedatapointsrepresentativeoftheshapeof
measured from the top of the mechanical layer in the anchor a surface-micromachined cantilever: (1) select two transitional
area (or region #2 in Fig. X2.2) to the top of the underlying edges, (2) obtain a 3-D data set, (3) ensure alignment, and (4)
layer (as shown in Fig. X2.1) and as specified in the reference select three data points. This procedure is presented inAppen-
(4) dix X1 for a bulk-micromachined cantilever.
H = the anchor etch depth (as shown in Fig. X2.1). The 4.3 To determine the strain gradient: (1) solve three equa-
amount the underlying layer is etched away in the z-direction tions for three unknowns, (2) plot the function with the data,
during the patterning of the sacrificial layer. and (3) calculate the strain gradient.
J = this dimension (as shown in Fig. X2.1) incorporates j ,
a
5. Significance and Use
j , j , and j , as shown in Figs. X2.3 and X2.4 (4)
b c d
j = the roughness of the underside of the suspended,
a
5.1 Strain gradient values are an aid in the design and
mechanicallayerinthe z-direction(asshowninFigs.X2.3and
fabrication of MEMS devices.
X2.4). This is due to the roughness of the topside of the
sacrificial layer.
6. Interferences
j = the tilting component of the suspended, mechanical
b
6.1 Measurements from cantilevers that are touching the
layer (as shown in Figs. X2.3 and X2.4)
underlying layer (as ascertained in Appendix X2) are not
j = the height in the z-direction of any residue present
c
accepted.
betweenthebottomofthesuspended,mechanicallayerandthe
top of the underlying layer (as shown in Figs. X2.3 and X2.4)
7. Apparatus
j = theroughnessofthetopsideoftheunderlyinglayer(as
d
7.1 Non-contact Optical Interferometer, capable of obtain-
shown in Figs. X2.3 and X2.4)
ing a topographical 3-D data set and has software that can
z = the z value (as shown in Fig. X2.2) of the point of
reg#1
export a 2-D data trace. Fig. 4 is a sketch of a suitable
maximum deflection along the cantilever beam with respect to
non-contact optical interferometer. However, any non-contact
the anchor lip
optical interferometer that has pixel-to-pixel spacings as speci-
z = a representative z value (as shown in Fig. X2.2) of
reg#2
fied in Table 1 and that is capable of performing the test
the group of points in region #2 within the large anchor area
procedurewithaverticalresolutionlessthan1nmispermitted.
3.2.6 Discussion—The symbols above are used throughout
The interferometer must be capable of measuring step heig
...