ISO/TR 7242:1981
(Main)Chemical analysis of light metals and their alloys — Statistical interpretation of inter-laboratory trials
Chemical analysis of light metals and their alloys — Statistical interpretation of inter-laboratory trials
This Technical Report constitutes an attempt to explain the numerical results of a statistical examination in the simplest possible way and to show how statistical results can be used in laboratory practice. This simplified method is applicable when the number of laboratories is not more than 20 and when the number of results per laboratory is not more than 10.
Analyse chimique des métaux et des alliages légers — Interprétation statistique des circuits interlaboratoires
General Information
Relations
Buy Standard
Standards Content (Sample)
INTERNATIONAL ORGANIZATION FOR STANDARDIZATlON.MEXflYHAPO~HAR OPrAHM3ALW l-i0 CTAH~APTM3ALWlM~ORGANlSATlON INTERNATIONALE DE NORMALISATION
Chemical analysis of light metals and their alloys -
Statistical interpretation of inter-laboratory trials
Analyse chimique des m&aux et des alll ’ages lhgers - In terprh ta tion s ta tis tique des circuits in terlabora toires
Technical Report 7242 was drawn up by Technical Committee ISO/TC 79, Light metals and their alloys, and has been approved by
the majority of its members.
Sub-committee ISO/TC 79/SC 1 considered it preferable to publish this document in the form of a Technical Report, as its purpose is
to provide information which could not be considered as a suitable subject for standardization but which is useful for users of stan-
dards confronted with the complex problems encountered during statistical studies resulting from round-robin, comparative analytical
trials.
0 Introduction
The purpose of inter-laboratory trials is to compare the results obtained in terms of two parameters : the methods and the
laboratories.
The following combinations can therefore be considered :
-
a method tested by several laboratories;
-
several methods tested within one laboratory;
-
two or more methods tested by several laboratories.
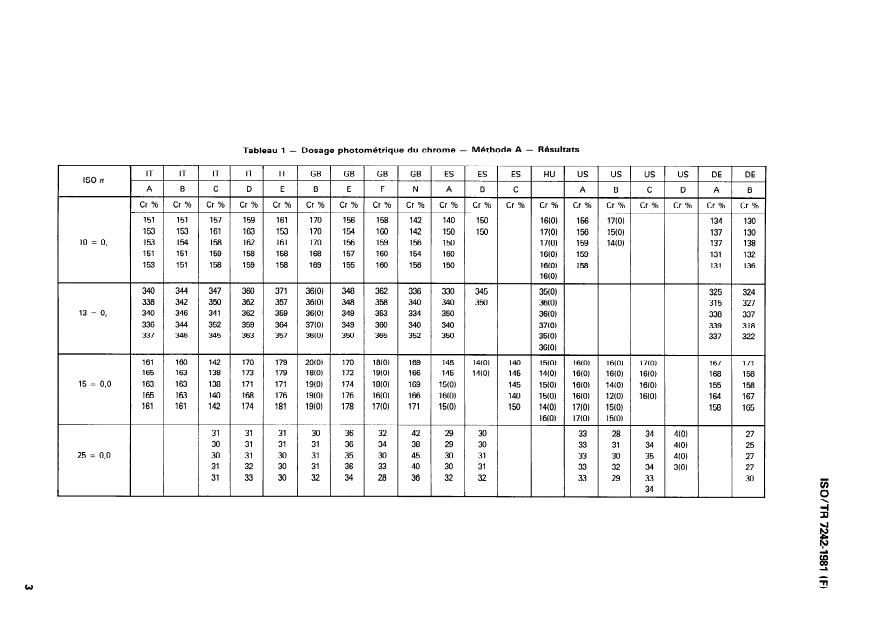
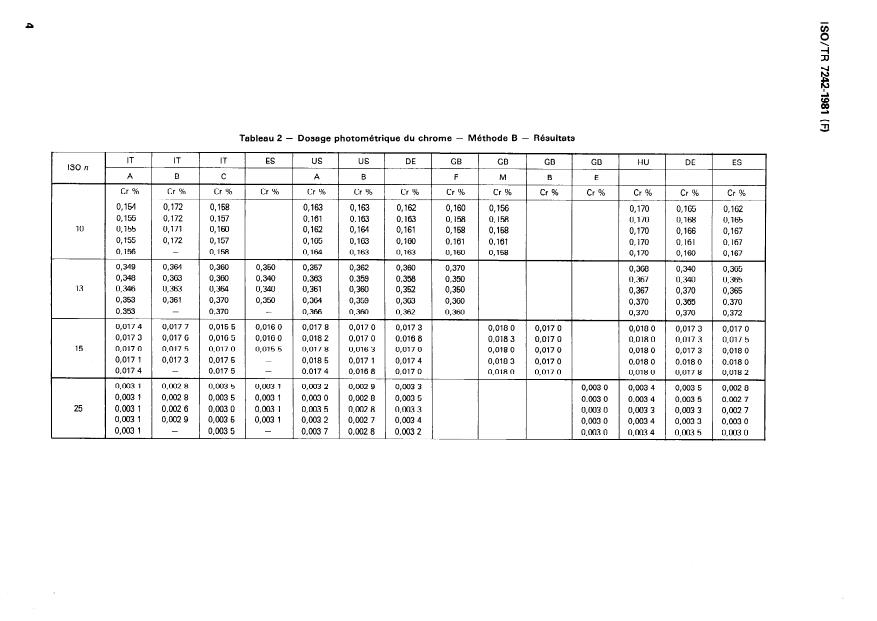
As an example, see tables 1, 2 and 3 relating to the determination of chromium.
Whichever combination is selected for the trial, interpretation of the results seeks to establish whether the recorded numerical dif-
ferences are mainly due to the influence of the parameter studied (laboratory, method) or whether they can be explained by the
dispersion observed between individual results (repeatability or experimental error). In all cases, the results of the statistical examina-
tion should be interpreted from an analytical viewpoint. The repeatability of a method can be sufficiently good for the small inter-
laboratory differences to be significant from the statistical point of view., although they can be considered negligible in practice. Con-
versely, poor repeatability does not imply that differences considered important by the user are significant.
Statistical interpretation, even when using very sophisticated calculation methods, has never corrected the failures of a method, nor
has it improved the results from a laboratory.
It is a tool leading very often to conclusions, the essential merit of which is objectivity.
UDC 669.7V.72 : 543 Ref. No. ISO/TR 7242-1981 (E)
spectrophotometric analysis,
determination of content, chromium,
Descriptors : metals, light alloys, chemical analysis, statistical analysis,
statistical tables.
Price based on 15 pages
---------------------- Page: 1 ----------------------
ISO/TR 7242-1981
(El
1 Scope and field of application
This Technical Report constitutes an attempt to explain the numerical results of a statistical examination in the simplest possible way
and to show how statistical results can be used in laboratory practice.
This simplified method is applicable when the number of laboratories is not more than 20 and when the number of results per
laboratory is not more than 10.
2 Symbols
: arithmetic mean of n results;
%l
s, : estimated standard deviation of y1 results;
: estimated standard deviation of the mean of n results : S,/,I%;
sx,
S,lX, : relative standard deviation or coefficient of variation, as a percentage.
NOTE - To add or subtract two standard deviations, determine the sum or difference of their squares and take the square root.
3 Example of interpretation of statistical parameters - Determination of chromium
Results of an inter-laboratory trial of two methods, A and B, for the determination of chromium are given. It is not intended to give a
complete interpretation of the results, but to show the possibilities of interpretation from the parameters established.
Individual results are given in tables 1 and 2.
The statistical parameters relating to the comparison of both methods are given in table 3. These parameters can be explained, or at
least translated into, more practical formulae without requiring recourse to basic statistical documents. Reference may be made to a
standardized method of calculating these parameters.
Table 4 summarizes explanations relative to the parameters given in table 3.
---------------------- Page: 2 ----------------------
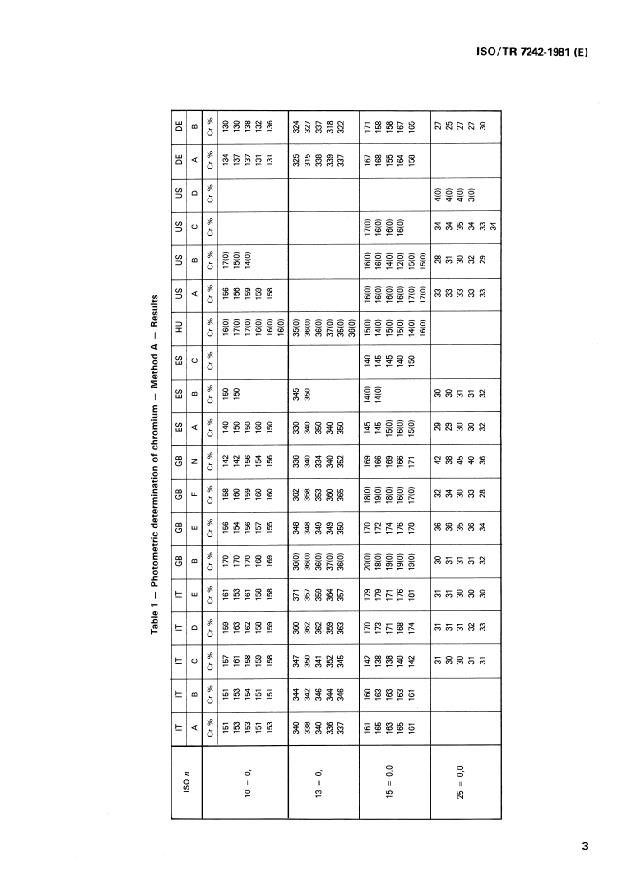
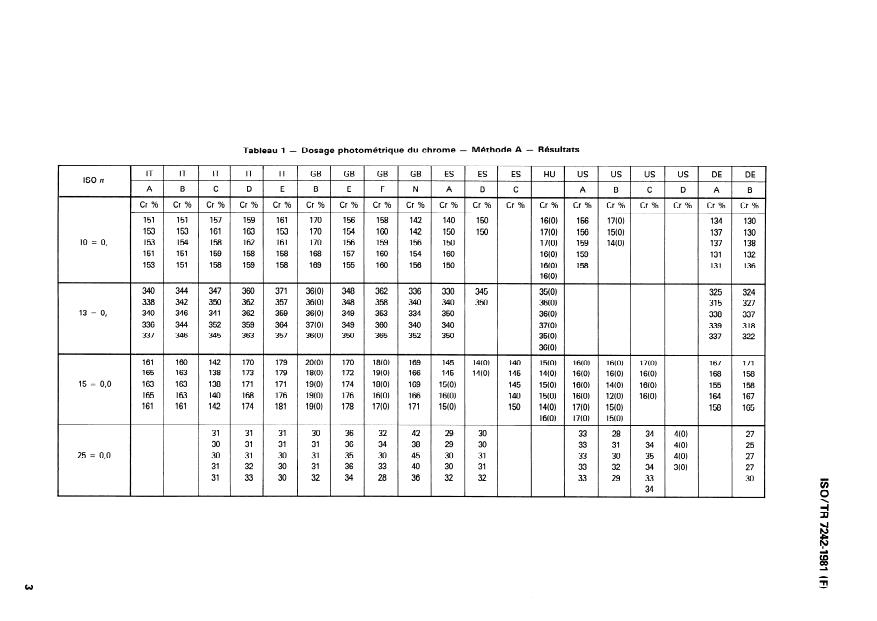
Table 1 - Photometric determination of chromium - Method A - Results
/
IT IT IT GB GB GB GB DE DE
IS0 n
A D E B E F N A B
+-l-+-P
I--
Cr % Cr % 1 Cr% Cr % Cr % Cr % Cr % Cr % Cr % Cr % 1 Cr % 1 Cr % 1 Cr % Cr % Cr %
151 151 157 159 161 170 156 158 142 140 150 l&O, 134 130
153 153 161 153 170 154 160 142 150 150 137 130
163 17(O)
10 = 0, 153 154 158 162 161 170 156 159 156 150 17(O) 137 138
151 151 159 158 158 168 157 160 154 160 16(O) 131 132
151 158 159 158 169 155 160 156 150 131 136
16(O)
16(O)
340 344 347 360 371 36(O) 348 362 336 345 35(O) 325 324
338 342 350 362 357 348 358 340 350
36(O) 36(O) 315 327
13 = 0, 340 346 341 362 359 36(O) 349 353 334 338 337
36(O)
360
336 344 352 359 364 37(O) 349 340 37(O) 339 318
346 345 363 357 350 365 352
36(O) 35(O) 337 322
36(O)
1
170
161 160 142 170 179 20(O) 18(O) 169 145 14(O) 140 15(O) 16(O) 16(O) 17(O) 167 171
165 163 138 173 179 172 166
18(O) 19(O) 145 -t4(0) 145 14(O) 16(O) 16(O) 16(O) 168 158
15 = 0,o 163 163 138 171 171 19(O) 174 18(O) 169 155 158
15(O) 145 15(O) 16(O) 14(O) WO)
163 140 176 166
165 168 176 WO) 16(O) 16(O) 140 15(O) 16(O) 12(O) 16(O) 164 167
161 161 142 174 181 178 171 158 165
19(O) 17(O) 15(O) 150 14(O) 17(O) 15(O)
16(O) 17(O) 15(O)
31 31 31 30 36 32 42 29 30 33 28 34 4(O) 27
30 31 31 31 36 34 38 29 30 33 31 34 25
4(O)
25 = 0,O 30 31 30 31 35 30 45 30 31 33 30 35 27
4(O)
31 32 30 31 36 33 40 30 31 33 32 34 3(O) 27
31 33 30 32 34 28 36 33 29 33 30
34
---------------------- Page: 3 ----------------------
m
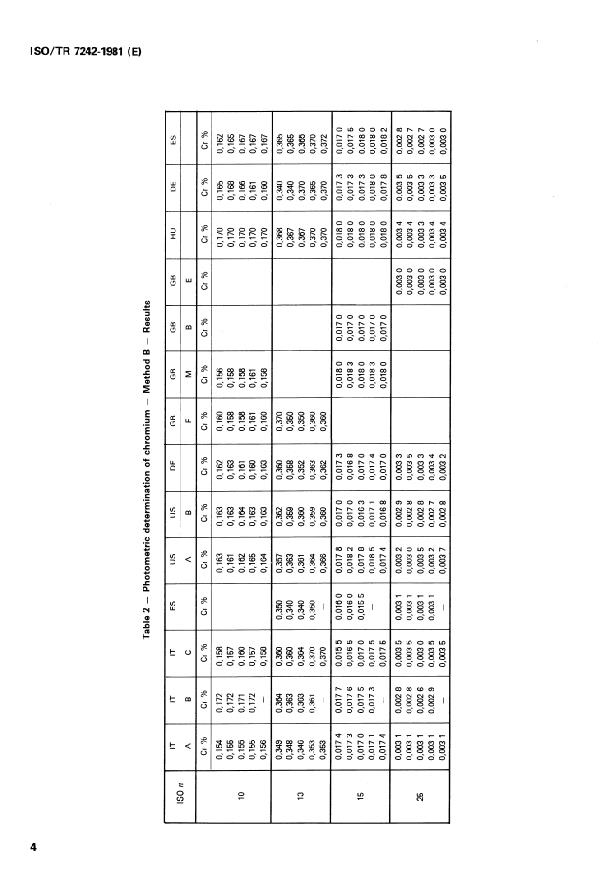
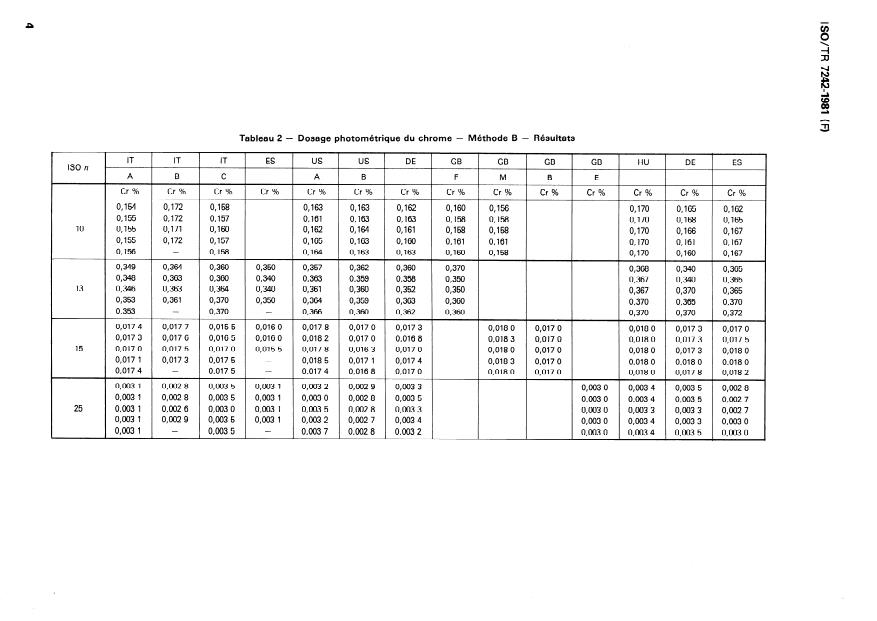
Photometric determination of chromium - Method B - Results
Table 2 -
IT IT IT ES us us DE GB GB GB GB HU DE ES
IS0 n
A B A F
C B M B E
Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr %
Cr % Cr % Cr % Cr % Cr % Cr %
/ 0,170 0,165 0,162
0,154 0,172 0,158 0,163 0,163 0,162 0,160 0,156
0,172 0,157 0,161 0,163 0,163 0,158 0,158 0,170 0,168 0,165
0,155
10 0,155 0,171 0,160 0,162 0,164 0,161 0,158 0,158 0,170 0,166 0,167
0,170 0,161 0,167
0,155 0,172 0,157 0,165 0,163 0,160 0,161 0,161
- 0,158 0,164 0,163 0,163 0,160 0,158 0,170 0,160 0,167
0,156
0,349 0,364 0,360 0,350 0,357 0,362 0,360 0,370 0,368 or=0 0,365
0,367 (m-0 0,365
0,348 0,363 0,360 0,340 0,363 0,359 0,358 0,350
0,3Jo 0,361 0,360 0,352 0,350 0,367 0,370 0,365
13 0,346 0,363 0,364
0,353 0,361 0,370 0,350 0,364 0,359 0,363 0,360 0,370 0,365 0,370
0,370 0,370 0,372
0,353 - 0,370 - 0,366 0,360 0,362 0,360
0,017 3 0,018 0 0,017 0 0,018 0 0,017 3 0,017 0
0,017 4 0,017 7 0,015 5 0,016 0 0,017 8 0,017 0
0,017 3 0,017 6 0,016 5 0,016 0 0,018 2 0,017 0 0,016 8 0,018 3 0,017 0 0,018 0 0,017 3 0,017 5
15 0,017 0 0,017 5 0,017 0 0,015 5 0,017 8 0,016 3 0,017 0 0,018 0 0,017 0 0,018 0 0,017 3 0,018 0
0,017 4 0,018 3 0,017 0 0,018 0 0,018 0 0,018 0
0,017 1 0,017 3 0,017 5 - 0,018 5 0,017 1
0,017 4 - 0,017 5 - 0,017 4 0,016 8 0,017 0 0,018 0 0,017 0 0,018 0 0,017 8 0,018 2
0,0031 0,0028 0,0035 0,0031 0,0032 0,0029 0,0033 0,003o 0,0034 0,003 5 0,0028
0,0031 0,003o 0,0028 0,0035 0,003o o,OO34 0,0035 0,0027
0,0031 0,0028 0,0035
25 0,0031 0,0026 0,003o 0,0031 0,0035 0,0028 .0,003 3 0,003o 0,0033 0,0033 0,0027
0,0034 0,003o 0,0034 0,0033 0,003o
0,0031 0,0029 0,0035 0,0031 0,0032 0,0027
o,OO31 - 0,0035 - 0,0037 0,0028 0,0032 0,003o 0,0034 0,0035 0,003o
---------------------- Page: 4 ----------------------
ISO/TR 7242-1981 (E)
Table 3 - Statistical parameters - Comparison of methods A and B
10 IS0 13 IS0 15 IS0 25
Sample IS0
440 R 2298 440 R 2298 440 R 2298 440
R 2298
77 54 68 53 89 57 70 53
N Number of observations
14 11
K Number of laboratories 16 11 14 11 18 12
0,003 231 0,003 141
x Arithmetic mean 0,153 89 0,162 5 0,347 83 0,359 7 0,016 17 0,017 17
Standard deviation
SW (within laboratories) 0,604 45 0,001 614 0,005 83 0,006 340 0,000 205 9 0,000 368 0,000 185 0,000 136
Sb (between laboratories) 0,009 44 0,004 916 0,011 73 0,006 249 0,001 335 0,000 573 0,000 325 0,000 244
0,001 485 0,000 680 0,000 374 0,000 280
St (total) 0,0104 5 0,605 174 0,013 1 0,008 902
S, (one pool) 0,010 15 0,004 998 0,012 78 0,008 737 0,001 457 0,000 664 0,000 365 0,000 271
Confidence level 99 %
0,000 992 0,000 749
St . tN - 1 + 0,027 69 0,013 84 0,034 8 0,023 84 0,003 93 0,001 81
0,030 80 0,016 40 0,039 5 0,028 21 0,004 30 0,002 11 0,001 126 0,000 887
St . tK - 1 zk
Confidence level 95 %
St . tN - 1 AI 0,020,85 0,010 38 0,026 2 0,017 88 0,002 96 0,001 36 0,000 747 0,000 562
St l tK - 1 f 0,022 27 0,011 53 0,028 3 0,019 83 0,003 13 0,001 50 0,000 808 0,000 624
Table 4 - Explanation of the statistical parameters figuring in table 3
Parameter
Significance Use
Estimate of the dispersion within laboratories (i.e.
Basic term for evaluation of “laboratory effects”
the repeatability). and “method effects ”.
Estimate of the effect of the factor studied If it has a significant value, it is important in the
(laboratory or method). Prior to this estimation, the estimation of the two parameters
observed dispersion between means has to be [(St and St, (K - III.
calculated, from which the contribution of S, to the
observed dispersion has to be subtracted.
It is independent of the number of measurements
carried out in each laboratory.
Only has meaning if Sb is significant. lt estimates the Very often, it is not physically different from Sb.
reproducibility related to a single measurement in Practically it does not decrease when the number of
one laboratory determinations n increases.
S2 = sg + s;
t
S, (SN would be more logical) Estimate of the standard deviation of N S, is more often used in this case.
measurements.
Only has meaning if Sb is not significant and then is
not significantly different from S, which has already
been computed.
St - t, (N -1) Confidence interval of the true value (at risk a) when Confidence interval of a single determination.
a = risk Sb is not significant and when only a single deter- (N - 1) is sufficiently high that t = 2,0 when
N-l = number of degrees of mination has been made. SN . ta (N - 1) would be a = 0,05.
freedom more logical.
St . t, (K - 1) Confidence interval of the true value (at risk a) Provides a confidence interval to be used in prac-
when Sb is significant and only a single determina- tice, and to compare data; t is given by Student ’s
a = risk
K-l = number of degrees of tion has been made. table and is a function of (K - 1).
freedom
---------------------- Page: 5 ----------------------
ISO/TR 7242-1981 (E)
may be
3. I Such inter-laboratory answers to be given to a number of questions
among which are :
a) Can it be considered that, for a given method, all laboratories have supplied the same result?
Are the average results for each method the same?
b)
confidence interval should be allocated to a result? Can this interval
c) When these questions have been answered,
proved by repeating the determination?
3.2 Effect of factor studied (laboratory effect)
To try to give an objective answer to the questions posed in 3.1, the statistical method relies on the following principle : comparison of
the dispersion of the mean results characterizing the factor studied with the experimental dispersion observed within the series of
results.
3.2.1 If the dispersion ratio is not sufficiently high, i.e. if it does not exceed a determined threshold given in a table ’), it cannot be
said that an additional dispersion has been introduced by the factor studied.
3.2.2 Conversely, if the dispersion ratio exceeds the determined threshold for the selected risk (significance level), the experimental
dispersion may be estimated from the observed dispersion of the mean values, and this can be subtracted in order to evaluate the
specific effect of the factor studied.
3.2.3 Referring to table 3, - sample IS0 13 - column A (case of a method used by several laboratories) :
S,,,, is the standard deviation allowing characterization of the dispersion within laboratories; it is the common experimental standard
deviation21 : it is 58 ppm for an average content of 3 480 ppm, i.e. I,7 % as a relative value.
for this sample will have an experimental dispersion characterized by a stan-
Each of the means of five values obtained laboratory
dard deviation of :
58
= 26 ppm
&
But the standard deviation characterizing the observed dispersion of mean values is 123 ppm (this does not appear in table 3).
‘= 22, which is greater than the threshold given in the Snedecor table, at a risk a = 0,05
and for the appropriate number of degrees of freedom.
the results differ from one laboratory to another with respect to the ex-
3.2.4 It can therefore be stated, at the risk selected, that
perimental dispersion. A laboratory effect can be observed. This effect is characterized in table 3 by Sb, such that :
‘2b = S?bserved between means - ?!!-
5
tly by one single I aboratory is chara standard deviation St(,) (called the standard
The mean of n results obtained subsequen
deviation of the reproducibility) such that
S2
= s2, +w
S2
b?)
n
measu rements times in order to
If Sb is proportionately larger than SW, as is very often the case, it is
the accuracy. St is never less than Sb.
when n = 5.
NOTE - lt should be noted that Szbserved beWeen meanS equals s2
bz)
Snedecor table.
1)
To be exact, a preliminary homogeneity test should be applied to the dispersion within laboratories.
a
6
---------------------- Page: 6 ----------------------
ISO/TR 7242-1981 (E)
3.2.5 In the case where statistical testing does not allow the affirmation that the observed mean dispersion is significantly greater
than the experimental dispersion, the laboratory effect cannot be calculated, and the dispersion affecting a subsequent result has to
be estimated from S, which is not significantly different from SW.
same popu
It is in fact considered that a II individual results belong to one lation, the dispe rsion of which is due only to experimental
error. The dispersion should then decrease with an increasing number of determinations.
3.3 Confidence intervals of results
Two confidence limits are thus obtained according to whether there is a laboratory effect or not.
For a selected level a, the following cases can be considered.
3.3.1
Case where there is no laboratory effect
in table 3 represents the confidence interval affecting one single result obtained by one laboratory (St is not
The term St I& (N _ ljlJ’
significantly different from S, or SW; these are three different estimates of the same dispersion). This interval decreases in the propor-
tion 1 /-Jn in the case of n determinations. In the example, this limit cannot be used because a laboratory effect exists.
3.3.2 Case where there is evidence of a laboratory effect
The term St [ k _ 111 of table 3 represents the confidence interval affecting one single result obtained by one laboratory; this interval
fix (
decreases in the case of n repetitions according to the formula
S’ \
sf = sg + -!L
n
In the example, this interval is practically independent of n since Sb (laboratory effect) is large with respect to SW.
In the preceding formulae
is the Student-Fischer variable;
*cY
k - 1 is the number of degrees of freedom of St when Sb is significant.
all the parameters men and in table 3. This method is rather time con-
3.4 There is a standardized method for calculating
suming and requires experience.
An extremely simplified method, requiring only elementary calculations but which leads to the same conclusions as the so-called “or-
thodox” method, is proposed.
This rapid method is applicable when the number of laboratories does not 20 and when the number of results
...
RAPPORT TECHNIQUE 7242
Publié 1981-06-01
INTERNATIONAL ORGANIZATION FOR STANDARDIZATION*ME~~YHAPO,QHA~~ OPrAHM3A~MR rl0 CTAH~APTM3AL&lM@ORGANlSATION INTERNATIONALE DE NORMALISATION
Analyse chimique des métaux et des alliages légers -
Interprétation statistique des circuits interlaboratoires
Chemical analysis of light metals and their alloys - S ta tis tical in terpre ta tion of in ter-labora tory trials
Le Rapport technique 7242 a été établi par le Comité technique ISO/TC 79, Métaux légers et leurs alliages, et approuvé par la majorité
de ses membres.
Le sous-comité ISO/TC 7WSC 1 a jugé opportun de soumettre la publication de ce document sous forme de Rapport technique, car
son but est de donner un ensemble de renseignements informatifs qui ne peut en aucun cas faire l’objet d’une normalisation, mais qui
vise à venir en aide aux utilisateurs de normes confrontés aux problèmes complexes rencontrés au cours des études statistiques réali-
sées pour le dépouillement des circuits d’analyse de comparaison.
0 introduction
Les circuits interlaboratoires visent à comparer les résultats obtenus en fonction des deux paramètres : méthodes et laboratoires.
Les différentes combinaisons ci-après peuvent être considérées :
-
une méthode essayée par plusieurs laboratoires;
- plusieurs méthodes essayées à l’intérieur d’un seul laboratoire;
- deux ou plusieurs méthodes essayées par plusieurs laboratoires.
À titre d’exemple, se reporter aux tableaux 1, 2 et 3 relatifs au dosage du chrome.
Quelle que soit la combinaison choisie pour l’essai, d’une facon très.générale, l’interprétation cherche à établir si les différences numé-
riques observées sont essentiellement dues à l’action du facteur étudié (laboratoire, méthode) ou bien si ces différences peuvent être
expliquées par la dispersion observée entre les résultats individuels (répétabilité ou erreur expérimentale). Dans tous les cas, les résul-
tats du test statistique restent à interpréter sous l’angle analytique. Une méthode peut en effet posséder une répétabilité suffisamment
bonne pour que de petites différences entre laboratoires soient significatives du point de vue statistique, bien que dans la pratique, ces
différences puissent être considérées comme négligeables. À l’inverse, une répétabilité mauvaise ne permet pas de rendre significati-
ves des différences pourtant importantes du point de vue de l’utilisateur.
L’interprétation statistique, même en utilisant des calculs très compliqués, n’a jamais corrigé les défauts d’une méthode ni amélioré les
résultats d’un laboratoire.
C’est un outil de travail qui permet très souvent d’aboutir à des conclusions dont le mérite essentiel est à nos yeux l’objectivité.
î
-
Réf. no : ISO/TR7242-1981 (FI
CDU 669.711.72 : 543
z
méthode spectrophotométrique, table
Descripteurs : métal, alliage léger, analyse chimique, analyse statistique, détermination, chrome,
statistique.
Prix basé sur 15 pages
---------------------- Page: 1 ----------------------
ISO/TR 7242-1981 (F)
1 Objet et domaine d’application
Le présent Rapport technique constitue une tentative pour expliquer aussi simplement que possible les résultats numériques d’un test
statistique et montrer comment les utiliser dans la pratique du laboratoire.
Cette méthode simplifiée est applicable lorsque le nombre de laboratoires ne dépasse pas 20 et lorsque le nombre de résultats par labo-
ratoire n’excède pas 10.
2 Notations utilisées
X, désigne la moyenne arithmétique de n résultats;
S, désigne l’écart-type estimé sur n résultats;
Sin désigne l’écart-type estimé de la moyenne de n résultats : S,lfi;
relatif ou le coefficient de variation, en pourcentage.
l’écart-type
NOTE on veut faire la somme ou la difference de deux écarts-types, on fait la somme ou la difference de leurs carrés et on en prend la racine.
- Quand
3 Exemples d’interprétation des paramètres statistiques - Dosage du chrome
Les résultats de comparaison interlaboratoire sont présentés pour deux méthodes A et B de dosage du chrome. II ne s’agit pas de faire
une interprétation complète de ce test, mais de montrer les possibilités d’interprétation des paramètres établis.
Les résultats individuels sont donnés dans les tableaux 1 et 2.
Le tableau 3 fournit les paramètres statistiques relatifs à ta comparaison des deux méthodes. Ces paramètres peuvent être explicités
ou tout au moins traduits en formules plus pratiques sans qu’on ait besoin d’avoir recours au document statistique de base. Pour cal-
culer ces paramètres, il existe une méthode normalisée à laquelle on pourra se référer.
Le tableau 4 résume les explications relatives aux paramètres donnés dans le tableau 3.
2
---------------------- Page: 2 ----------------------
Tableau 1 - Dosage photométrique du chrome - Méthode A - Résultats
-
IT IT IT IT IT GB GB GB GB ES ES ES HU us us us us DE DE
ISO n
A B C D E B E F N A B C A B C D A B
Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % -Cr % Cr % Cr % Cr % Cr % Cr % Cr %
151 151 157 159 161 170 156 158 142 140 150 16(O) 156 17(O) 134 130
170 154 160 142 150
153 153 161 163 153 150 17(O) 156 15(O) 137 130
10 = 0, 153 154 158 162 161 170 156 159 156 150 159 137 138
17(O) 14(O)
151 151 159 158 158 168 157 160 154 160 160 159 131 132
151 158 169 155 160 156 150 131
153 158 159 16(O) 158 136
16(O)
340 347 360 371 348 362 336 330 345 -35101 325 324
36(O)
338 342 350 362 357 36(O) 348 358 340 340 350 36(O) 315 327
13 = 0, 340 346 341 362 359 349 353 334 350 338 337
36(O) 36(O)
336 344 352 359 364 37(O) 349 360 340 339 318
37(O)
337 346 345 363 357 36(O) 350 365 352 350 3510) 337 322
36(O)
161 160 142 170 179 2W) 170 18(O) 169 145 14(O) 140 -150 16(O) 17(O) 167 171
16(O)
172
165 163 138 173 179 18(O) 19(O) 166 145 14(O) 145 14(O) 16(O) 16(O) 16(O) 168 158
15 = 0,o 163 163 138 171 171 174 169 145 155
19(O) 18(O) 15(O) 15(O) 16(O) 14(O) 16(O) 158
165 163 140 168 176 19(O) 176 MO) 166 16(O) 140 15(O) 16(O) 12(O) 16(O) 164 167
161 161 142 174 181 178 171 150
19(O) 17(O) 15(O) 14(O) 17(O) 15(O) 158 165
16(O) 17(O) 15(O)
31 31 31 30 36 32 42 29 30 33 28 27
30 31 31 31 36 34 38 29 30 33 31 25
35 30 45 30 31
25 = 0,O 30 31 30 31 33 30 27
30 31 36 33 40 30 31 33 32 27
31 32
31 33 30 32 34 28 36 32 32 33 29 30
---------------------- Page: 3 ----------------------
- Dosage photométrique du chrome - Méthode B - Résultats
Tableau 2
IT IT IT ES us us DE GB GB GB GB HU DE ES
ISO n ,
A
B C A B F M B E
Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr %
0,154 0,172 0,158 0,163 0,163 0,162 0,160 0,156 0,170 0,165 0,162
0,158 0,158
0,155 0,172 0,157 0,161 0,163 0,163 0,170 0,168 0,165
0,161 0,158
10 0,155 0,171 0,160 0,162 0,164 0,158 0,170 0,166 0,167
0,165 0,163 0,160 0,161 0,161 0,170 0,161 0,167
0,155 0,172 0,157
0,156 - 0,158 0,164 0,163 0,163 0,160 0,158 0,170 0,160 0,167
0,360 0,370
0,349 0,364 0,360 0,350 0,357 0,362 0,368 o,=o 0,365
0,360 or=0 0,363 0,359 0,358 0,350 0,367 0,340 0,365
os@ 0,363
0,350
13 0,346 0,363 0,364 o,= 0,361 0,360 0,352 0,367 0,370 0,365
0,350 0,364 0,359 0,363 0,360 0,370
0,353 0,361 0,370 0,370 0,365
0,353 - 0,370 - 0,366 0,360 0,362 0,360 0,370 0,370 0,372
0,018 0 0,017 3 0,017 0
0,017 4 0,017 7 0,015 5 0,016 0 0,017 8 0,017 0 0,017 3 0,018 0 0,017 0
0,017 0 0,016 8 0,018 3 0,017 0 0,018 0 0,017 3 0,017 5
0,017 3 0,017 6 0,016 5 0,016 0 0,018 2
15 0,017 0 0,017 5 0,017 0 0,015 5 0,017 8 0,016 3 0,017 0 0,018 0 0,017 3 0,018 0
0,018 0 0,017 0
0,018 3 0,017 0 0,018 0 0,018 0 0,018 0
0,017 1 0,017 3 0,017 5 - 0,018 5 0,017 1 0,017 4
8 0,018 2
0,017 5 - 0,017 4 0,016 8 0,017 0 0,018 0 0,017 0 0,018 0 0,017
0,017 4 -
0,003o 0,0034 0,003 5 0,0028
0,0031 0,0028 0,0035 0,0031 0,0032 0,0029 0,0033
0,0028 0,0035
0,0031 0,0028 0,0035 0,0031 0,003o 0,003o 0,0034 0,0035 0,0027
0,0026 0,003o 0,0031 0,0035 0,0028 0,0033 0,0027
25 0,0031 0,003o 0,0033 0,0033
0,0031 0,0029 0,0035 0,0031 0,0032 0,0027 0,0034 0,003o 0,0034 0,0033 0,003o
0,0035 - 0,0037 0,0028 0,0032
0,0031 - 0,003o 0,0034 0,0035 0,003o
---------------------- Page: 4 ----------------------
ISO/TR 7242-1981 (F)
Tableau 3
- Paramètres statistiques - Comparaison des deux méthodes A et B
ISO 10 ISO 13
ISO 15 ISO 25
Échantillon
R 2298 440 R 2298 440
R 2298 440 R 2298 440
--
N Nombre d’observations
77 54 68 53 89 57 70
53
K Nombre de laboratoires 16 11
14 11 18 12 14 11
x Moyenne arithmétique
0,153 89 0,162 5 0,347 83 0,359 7 0,016 17
0,017 17 0,003 231 0,003 141
Écart-type
S,,,, (a l’intérieur des laboratoires)
0,004 45 0,001 614 0,065 83 0,006 340 0,000 205 9 0,000 368 0,000 185
0,000 136
Sb (entre laboratoires) 0,009 44 0,004 916
0,011 73 0,006 249 0,001 335 0,000 573 0,000 325 0,000 244
St (total) 0,0104 5 0,005 174 0,013 1
0,008 902 0,001485 0,000 680 0,ooo 374 0,000 280
S, (one pool)
0,010 15 0,004 998 0,012 78 0,008 737 0,901 457 0,000 664 0,000 365
0,000 271
Limites de confiance 99 %
St . tN - 1 k
0,027 69 0,013 84 0,034 8 0,023 84 0,003 93 0,001 81 0,ooo 992 0,ooo 749
St ’ tK - 1 + 0,030 80 0,016 40 0,039 5 0,028 21
0,004 30 0,002 11 0,001 126 0,ooo 887
l
Limites de confiance 95 %
St . tN - 1 f
St . tK - 1 +
Tableau 4 - Explications relatives aux paramètres statistiques figurant au tableau 3
Paramètres Signification Utilisation
I
Caractérise la dispersion à l’intérieur des laboratoires Terme de référence pour évaluer l’effet laboratoire
s,
(c’est la répétabilité). ou l’effet méthode.
I
Caractérise l’effet du facteur étudié (laboratoire ou S’il est significatif, il constitue un terme important
Sb
méthode). Pour l’estimer, il faut au préalable calcu- dans l’estimation de deux autres paramètres
ler la dispersion observée entre les moyennes, et [(St et S,, K - 1 Il.
retrancher à cette dispersion celle qui est caractéri-
sée par S,.
II est indépendant du nombre de mesures effectuées
dans chaque laboratoire.
N’a de signification que si Sb existe; c’est l’écart- Dans de nombreux cas, il n’est pas «physiquement»
St
type relatif à une seule mesure faite par un seul labo- différent de Sb et peu affecté par le nombre de répé-
titions n.
ratoire : reproductibilité (pour une mesure)
S2 = s; + s;
t
S, (SN serait plus logique) Écart-type de l’ensemble des N résultats. On utilise plus souvent S,.
N’a de signification que si Sb n’existe pas. II n’est
pas alors différent de S, qu’on a déjà forcément cal-
culé.
St - t, (N - 1) Caractérise l’intervalle de confiance de la vraie Établissement de l’intervalle de confiance d’un résul-
valeur (au risque a) lorsque Sb n’est pas significatif
a = risque tat; (N - 1) est suffisamment élevé en général pour
N -1 = d.d.1. et qu’on n’a fait qu’une détermination. que t = 2,0 pour a = 0,05.
SN . t, (N - 1) serait plus logique.
St - t, (K - 1) Caractérise l’intervalle de confiance de la vraie Donne un intervalle de confiance réaliste servant à
a= risque valeur (au risque a) lorsque Sb est significatif et comparer des valeurs entre elles; t est fonction de
K - 1 = d.d.1. qu’on a fait une seule détermination. (K - 1); (donné par la table de Student).
---------------------- Page: 5 ----------------------
ISO/TR 7242-1981 (F)
3.1 Un tel circuit inter-laboratoire permet de répondre objectivement à un certain nombre de questions que peuvent se poser les
entre autres :
analystes,
a) Pour une méthode donnée, peut-on considérer que tous les laboratoires ont fourni le même résultat?
Les résultats moyens correspondant à chaque méthode sont-ils les mêmes?
b)
c) Lorsqu’on a répondu à ces
questions, quel in te de confiance conviendra-t-il d’affecter à un résultat? Peut-on ou non amé-
liorer cet intervalle en effectua nt des répétitions
3.2 Effet du facteur étudié (effet laboratoire)
Pour tenter de répondre objectivement à ces questio lns, la méthode statistique utilise le principe suivant : comparer la dispersio n des
résultats moyens caractérisant le facteur étudié à la dispersion expérimentale observée à l’intérieur des séries de résultats.
3.2.1 Si le rapport de ces dispersions n’est pas
su ffisamment grand, c’est-à-dire s’il ne dépasse pas un certain seuil donné par une
table’), on ne peut pas dire que le facteur étudié a introduit une dispersion supplémentaire.
3.2. 2 Par contre, si le rapport des d ispersions dépasse le seuil fixé, au risque choisi, on peut alors estimer d ans la dispersion o lbservée
des moyennes, quelle est la part de la dispersion expér
‘imentale, et la retrancher de facon à estimer l’effet propre du facteur étudié.
,
3.2.3 Si l’on se rapporte au tableau 3, échantillon ISO 13 - colonne A (cas d’une méthode utilisée par plusieurs laboratoires) :
S, est l’écart-type qui permet de caractériser la d à l’intérieur des laboratoires; c ‘est l’écart-type expérimental comm un2) :
ispersion
il est de 58 ppm pour une teneur moyenne de 3 , soit 1,7 % en valeur relative.
480 PPm
Chacune des moyennes de cinq valeurs obtenues par un laboratoire pour cet échantillon aura une dispersion expérimentale caractéri-
sée par un écart-type de :
58
- = 26 ppm
6
Or l’écart-type qui caractérise la dispersion observée des moyennes est de 123 ppm (ne figure pas au tableau 3). Le rapport des deux
123 2
0,05 et pour les nombres de degrés de
dispersions : - = 22 est supérieur au seuil donné par la table de Snedecor au risque a =
i 26 1
liberté appropriés.
3.2.4 On peut donc affirmer, au risque les résultats son t différents d’un laboratoire à eu égard à la
choisi de se tromper,
que
dispersion expérimen tale : il y a un effet laboratoire. Cet effet est caractérisé dans le tableau 3 par sb, tel que
S2
% = ‘ibservé entre moyennes - w
5
résultats ultérieurement par un écart-type écart-type de
Une moyenne de n obtenue par un seul laboratoire sera caractérisée St(,) (dit
reproductibilité) tel que :
S2
=s;+w
S2
?n)
n
Si, comme c’est assez souvent le t à rien de faire plusieurs répé-
cas, Sb est relativement grand par rapport à S,, il ne sert pratiquemen
titions dans le but d’améliorer la précision. De toute facon, St ne peut jamais être inf érieur à sb.
NOTE - 11 y a lieu de remarquer que ce qui a été appelé S~bse,.,,6 entre moyennes n’est autre que s2 f( ) quand n = 5.
n
1) Table de Snedecor.
2) En toute rigueur, il faut appliquer un test préliminaire d’homogénéité des dispersions à l’intérieur des laboratoires.
6
---------------------- Page: 6 ----------------------
ISO/TR 7242-1981 (F)
3.2.5 Dans le cas où le test statistique n’a pas permis d’affirmer que la dispersion observée des moyennes est significativement supé-
rieure à la dispersion expérimentale, on ne peut pas calculer d’effet laboratoire, et la dispersion qui affectera un résultat ultérieur sera
établie à partir de S, qui n’est pas significativement différent de S,.
On considère en fait que tous les résultats individuels font partie d’une seule et même populatio n dont persi on n’est due qu’à
bre de répétitions.
l’erreur expérimentale. Cette dispersion va alors dimin uer en fonction du nom
33 . Intervalles de confiance des résultats
On aboutit donc à deux limites de confiance, suivant qu’il existe ou non un effet de laboratoire.
Pour un seuil de probabilité a choisi, on considérera les cas suivants.
3.3.1 Cas où il n’y a pas d’effet laboratoire
1) du tablea u3 représente l’intervalle de confiance affectant un seul résu ltat obtenu par u n laboratoire (St n ‘est pas signi-
St [t
a, (N - ld
ficativement différent de ni de S,,,,. Ce sont trois estimations différentes de la même dispersion) . Cet intervalle diminue comme Ilfi
srl
dans le cas de n répétitions. Dans l’exemple, cette limite n’est pas utilisable puisque l’effet laboratoire existe.
Cas où un effet laboratoire a été mis en évidence
3.3.2
St [ta, (k _I)l du tableau 3 représente l’intervalle de confiance affectant un seul résultat obtenu par un laboratoire; cet intervalle dimi-
nuera dans le cas de n répétitions, suivant la formule :
S2
=s;+L
S2
t
n
Dans l’exemple, cet intervalle est pratiquement indépendant de n puisque Sb (effet laboratoire) est grand devant S,.
Dans les formules précédentes,
est la variable Student-Fischer;
ta
k -1 est le nombre de degrés de liberté de St lorsque Sb est significatif.
34 . II existe une méthode normalisée pour calculer tous les paramètres mentionnés et utilisés dans le tableau 3. Cette méthode est
assez laborieuse et requiert une certaine h
...
RAPPORT TECHNIQUE 7242
Publié 1981-06-01
INTERNATIONAL ORGANIZATION FOR STANDARDIZATION*ME~~YHAPO,QHA~~ OPrAHM3A~MR rl0 CTAH~APTM3AL&lM@ORGANlSATION INTERNATIONALE DE NORMALISATION
Analyse chimique des métaux et des alliages légers -
Interprétation statistique des circuits interlaboratoires
Chemical analysis of light metals and their alloys - S ta tis tical in terpre ta tion of in ter-labora tory trials
Le Rapport technique 7242 a été établi par le Comité technique ISO/TC 79, Métaux légers et leurs alliages, et approuvé par la majorité
de ses membres.
Le sous-comité ISO/TC 7WSC 1 a jugé opportun de soumettre la publication de ce document sous forme de Rapport technique, car
son but est de donner un ensemble de renseignements informatifs qui ne peut en aucun cas faire l’objet d’une normalisation, mais qui
vise à venir en aide aux utilisateurs de normes confrontés aux problèmes complexes rencontrés au cours des études statistiques réali-
sées pour le dépouillement des circuits d’analyse de comparaison.
0 introduction
Les circuits interlaboratoires visent à comparer les résultats obtenus en fonction des deux paramètres : méthodes et laboratoires.
Les différentes combinaisons ci-après peuvent être considérées :
-
une méthode essayée par plusieurs laboratoires;
- plusieurs méthodes essayées à l’intérieur d’un seul laboratoire;
- deux ou plusieurs méthodes essayées par plusieurs laboratoires.
À titre d’exemple, se reporter aux tableaux 1, 2 et 3 relatifs au dosage du chrome.
Quelle que soit la combinaison choisie pour l’essai, d’une facon très.générale, l’interprétation cherche à établir si les différences numé-
riques observées sont essentiellement dues à l’action du facteur étudié (laboratoire, méthode) ou bien si ces différences peuvent être
expliquées par la dispersion observée entre les résultats individuels (répétabilité ou erreur expérimentale). Dans tous les cas, les résul-
tats du test statistique restent à interpréter sous l’angle analytique. Une méthode peut en effet posséder une répétabilité suffisamment
bonne pour que de petites différences entre laboratoires soient significatives du point de vue statistique, bien que dans la pratique, ces
différences puissent être considérées comme négligeables. À l’inverse, une répétabilité mauvaise ne permet pas de rendre significati-
ves des différences pourtant importantes du point de vue de l’utilisateur.
L’interprétation statistique, même en utilisant des calculs très compliqués, n’a jamais corrigé les défauts d’une méthode ni amélioré les
résultats d’un laboratoire.
C’est un outil de travail qui permet très souvent d’aboutir à des conclusions dont le mérite essentiel est à nos yeux l’objectivité.
î
-
Réf. no : ISO/TR7242-1981 (FI
CDU 669.711.72 : 543
z
méthode spectrophotométrique, table
Descripteurs : métal, alliage léger, analyse chimique, analyse statistique, détermination, chrome,
statistique.
Prix basé sur 15 pages
---------------------- Page: 1 ----------------------
ISO/TR 7242-1981 (F)
1 Objet et domaine d’application
Le présent Rapport technique constitue une tentative pour expliquer aussi simplement que possible les résultats numériques d’un test
statistique et montrer comment les utiliser dans la pratique du laboratoire.
Cette méthode simplifiée est applicable lorsque le nombre de laboratoires ne dépasse pas 20 et lorsque le nombre de résultats par labo-
ratoire n’excède pas 10.
2 Notations utilisées
X, désigne la moyenne arithmétique de n résultats;
S, désigne l’écart-type estimé sur n résultats;
Sin désigne l’écart-type estimé de la moyenne de n résultats : S,lfi;
relatif ou le coefficient de variation, en pourcentage.
l’écart-type
NOTE on veut faire la somme ou la difference de deux écarts-types, on fait la somme ou la difference de leurs carrés et on en prend la racine.
- Quand
3 Exemples d’interprétation des paramètres statistiques - Dosage du chrome
Les résultats de comparaison interlaboratoire sont présentés pour deux méthodes A et B de dosage du chrome. II ne s’agit pas de faire
une interprétation complète de ce test, mais de montrer les possibilités d’interprétation des paramètres établis.
Les résultats individuels sont donnés dans les tableaux 1 et 2.
Le tableau 3 fournit les paramètres statistiques relatifs à ta comparaison des deux méthodes. Ces paramètres peuvent être explicités
ou tout au moins traduits en formules plus pratiques sans qu’on ait besoin d’avoir recours au document statistique de base. Pour cal-
culer ces paramètres, il existe une méthode normalisée à laquelle on pourra se référer.
Le tableau 4 résume les explications relatives aux paramètres donnés dans le tableau 3.
2
---------------------- Page: 2 ----------------------
Tableau 1 - Dosage photométrique du chrome - Méthode A - Résultats
-
IT IT IT IT IT GB GB GB GB ES ES ES HU us us us us DE DE
ISO n
A B C D E B E F N A B C A B C D A B
Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % -Cr % Cr % Cr % Cr % Cr % Cr % Cr %
151 151 157 159 161 170 156 158 142 140 150 16(O) 156 17(O) 134 130
170 154 160 142 150
153 153 161 163 153 150 17(O) 156 15(O) 137 130
10 = 0, 153 154 158 162 161 170 156 159 156 150 159 137 138
17(O) 14(O)
151 151 159 158 158 168 157 160 154 160 160 159 131 132
151 158 169 155 160 156 150 131
153 158 159 16(O) 158 136
16(O)
340 347 360 371 348 362 336 330 345 -35101 325 324
36(O)
338 342 350 362 357 36(O) 348 358 340 340 350 36(O) 315 327
13 = 0, 340 346 341 362 359 349 353 334 350 338 337
36(O) 36(O)
336 344 352 359 364 37(O) 349 360 340 339 318
37(O)
337 346 345 363 357 36(O) 350 365 352 350 3510) 337 322
36(O)
161 160 142 170 179 2W) 170 18(O) 169 145 14(O) 140 -150 16(O) 17(O) 167 171
16(O)
172
165 163 138 173 179 18(O) 19(O) 166 145 14(O) 145 14(O) 16(O) 16(O) 16(O) 168 158
15 = 0,o 163 163 138 171 171 174 169 145 155
19(O) 18(O) 15(O) 15(O) 16(O) 14(O) 16(O) 158
165 163 140 168 176 19(O) 176 MO) 166 16(O) 140 15(O) 16(O) 12(O) 16(O) 164 167
161 161 142 174 181 178 171 150
19(O) 17(O) 15(O) 14(O) 17(O) 15(O) 158 165
16(O) 17(O) 15(O)
31 31 31 30 36 32 42 29 30 33 28 27
30 31 31 31 36 34 38 29 30 33 31 25
35 30 45 30 31
25 = 0,O 30 31 30 31 33 30 27
30 31 36 33 40 30 31 33 32 27
31 32
31 33 30 32 34 28 36 32 32 33 29 30
---------------------- Page: 3 ----------------------
- Dosage photométrique du chrome - Méthode B - Résultats
Tableau 2
IT IT IT ES us us DE GB GB GB GB HU DE ES
ISO n ,
A
B C A B F M B E
Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr % Cr %
0,154 0,172 0,158 0,163 0,163 0,162 0,160 0,156 0,170 0,165 0,162
0,158 0,158
0,155 0,172 0,157 0,161 0,163 0,163 0,170 0,168 0,165
0,161 0,158
10 0,155 0,171 0,160 0,162 0,164 0,158 0,170 0,166 0,167
0,165 0,163 0,160 0,161 0,161 0,170 0,161 0,167
0,155 0,172 0,157
0,156 - 0,158 0,164 0,163 0,163 0,160 0,158 0,170 0,160 0,167
0,360 0,370
0,349 0,364 0,360 0,350 0,357 0,362 0,368 o,=o 0,365
0,360 or=0 0,363 0,359 0,358 0,350 0,367 0,340 0,365
os@ 0,363
0,350
13 0,346 0,363 0,364 o,= 0,361 0,360 0,352 0,367 0,370 0,365
0,350 0,364 0,359 0,363 0,360 0,370
0,353 0,361 0,370 0,370 0,365
0,353 - 0,370 - 0,366 0,360 0,362 0,360 0,370 0,370 0,372
0,018 0 0,017 3 0,017 0
0,017 4 0,017 7 0,015 5 0,016 0 0,017 8 0,017 0 0,017 3 0,018 0 0,017 0
0,017 0 0,016 8 0,018 3 0,017 0 0,018 0 0,017 3 0,017 5
0,017 3 0,017 6 0,016 5 0,016 0 0,018 2
15 0,017 0 0,017 5 0,017 0 0,015 5 0,017 8 0,016 3 0,017 0 0,018 0 0,017 3 0,018 0
0,018 0 0,017 0
0,018 3 0,017 0 0,018 0 0,018 0 0,018 0
0,017 1 0,017 3 0,017 5 - 0,018 5 0,017 1 0,017 4
8 0,018 2
0,017 5 - 0,017 4 0,016 8 0,017 0 0,018 0 0,017 0 0,018 0 0,017
0,017 4 -
0,003o 0,0034 0,003 5 0,0028
0,0031 0,0028 0,0035 0,0031 0,0032 0,0029 0,0033
0,0028 0,0035
0,0031 0,0028 0,0035 0,0031 0,003o 0,003o 0,0034 0,0035 0,0027
0,0026 0,003o 0,0031 0,0035 0,0028 0,0033 0,0027
25 0,0031 0,003o 0,0033 0,0033
0,0031 0,0029 0,0035 0,0031 0,0032 0,0027 0,0034 0,003o 0,0034 0,0033 0,003o
0,0035 - 0,0037 0,0028 0,0032
0,0031 - 0,003o 0,0034 0,0035 0,003o
---------------------- Page: 4 ----------------------
ISO/TR 7242-1981 (F)
Tableau 3
- Paramètres statistiques - Comparaison des deux méthodes A et B
ISO 10 ISO 13
ISO 15 ISO 25
Échantillon
R 2298 440 R 2298 440
R 2298 440 R 2298 440
--
N Nombre d’observations
77 54 68 53 89 57 70
53
K Nombre de laboratoires 16 11
14 11 18 12 14 11
x Moyenne arithmétique
0,153 89 0,162 5 0,347 83 0,359 7 0,016 17
0,017 17 0,003 231 0,003 141
Écart-type
S,,,, (a l’intérieur des laboratoires)
0,004 45 0,001 614 0,065 83 0,006 340 0,000 205 9 0,000 368 0,000 185
0,000 136
Sb (entre laboratoires) 0,009 44 0,004 916
0,011 73 0,006 249 0,001 335 0,000 573 0,000 325 0,000 244
St (total) 0,0104 5 0,005 174 0,013 1
0,008 902 0,001485 0,000 680 0,ooo 374 0,000 280
S, (one pool)
0,010 15 0,004 998 0,012 78 0,008 737 0,901 457 0,000 664 0,000 365
0,000 271
Limites de confiance 99 %
St . tN - 1 k
0,027 69 0,013 84 0,034 8 0,023 84 0,003 93 0,001 81 0,ooo 992 0,ooo 749
St ’ tK - 1 + 0,030 80 0,016 40 0,039 5 0,028 21
0,004 30 0,002 11 0,001 126 0,ooo 887
l
Limites de confiance 95 %
St . tN - 1 f
St . tK - 1 +
Tableau 4 - Explications relatives aux paramètres statistiques figurant au tableau 3
Paramètres Signification Utilisation
I
Caractérise la dispersion à l’intérieur des laboratoires Terme de référence pour évaluer l’effet laboratoire
s,
(c’est la répétabilité). ou l’effet méthode.
I
Caractérise l’effet du facteur étudié (laboratoire ou S’il est significatif, il constitue un terme important
Sb
méthode). Pour l’estimer, il faut au préalable calcu- dans l’estimation de deux autres paramètres
ler la dispersion observée entre les moyennes, et [(St et S,, K - 1 Il.
retrancher à cette dispersion celle qui est caractéri-
sée par S,.
II est indépendant du nombre de mesures effectuées
dans chaque laboratoire.
N’a de signification que si Sb existe; c’est l’écart- Dans de nombreux cas, il n’est pas «physiquement»
St
type relatif à une seule mesure faite par un seul labo- différent de Sb et peu affecté par le nombre de répé-
titions n.
ratoire : reproductibilité (pour une mesure)
S2 = s; + s;
t
S, (SN serait plus logique) Écart-type de l’ensemble des N résultats. On utilise plus souvent S,.
N’a de signification que si Sb n’existe pas. II n’est
pas alors différent de S, qu’on a déjà forcément cal-
culé.
St - t, (N - 1) Caractérise l’intervalle de confiance de la vraie Établissement de l’intervalle de confiance d’un résul-
valeur (au risque a) lorsque Sb n’est pas significatif
a = risque tat; (N - 1) est suffisamment élevé en général pour
N -1 = d.d.1. et qu’on n’a fait qu’une détermination. que t = 2,0 pour a = 0,05.
SN . t, (N - 1) serait plus logique.
St - t, (K - 1) Caractérise l’intervalle de confiance de la vraie Donne un intervalle de confiance réaliste servant à
a= risque valeur (au risque a) lorsque Sb est significatif et comparer des valeurs entre elles; t est fonction de
K - 1 = d.d.1. qu’on a fait une seule détermination. (K - 1); (donné par la table de Student).
---------------------- Page: 5 ----------------------
ISO/TR 7242-1981 (F)
3.1 Un tel circuit inter-laboratoire permet de répondre objectivement à un certain nombre de questions que peuvent se poser les
entre autres :
analystes,
a) Pour une méthode donnée, peut-on considérer que tous les laboratoires ont fourni le même résultat?
Les résultats moyens correspondant à chaque méthode sont-ils les mêmes?
b)
c) Lorsqu’on a répondu à ces
questions, quel in te de confiance conviendra-t-il d’affecter à un résultat? Peut-on ou non amé-
liorer cet intervalle en effectua nt des répétitions
3.2 Effet du facteur étudié (effet laboratoire)
Pour tenter de répondre objectivement à ces questio lns, la méthode statistique utilise le principe suivant : comparer la dispersio n des
résultats moyens caractérisant le facteur étudié à la dispersion expérimentale observée à l’intérieur des séries de résultats.
3.2.1 Si le rapport de ces dispersions n’est pas
su ffisamment grand, c’est-à-dire s’il ne dépasse pas un certain seuil donné par une
table’), on ne peut pas dire que le facteur étudié a introduit une dispersion supplémentaire.
3.2. 2 Par contre, si le rapport des d ispersions dépasse le seuil fixé, au risque choisi, on peut alors estimer d ans la dispersion o lbservée
des moyennes, quelle est la part de la dispersion expér
‘imentale, et la retrancher de facon à estimer l’effet propre du facteur étudié.
,
3.2.3 Si l’on se rapporte au tableau 3, échantillon ISO 13 - colonne A (cas d’une méthode utilisée par plusieurs laboratoires) :
S, est l’écart-type qui permet de caractériser la d à l’intérieur des laboratoires; c ‘est l’écart-type expérimental comm un2) :
ispersion
il est de 58 ppm pour une teneur moyenne de 3 , soit 1,7 % en valeur relative.
480 PPm
Chacune des moyennes de cinq valeurs obtenues par un laboratoire pour cet échantillon aura une dispersion expérimentale caractéri-
sée par un écart-type de :
58
- = 26 ppm
6
Or l’écart-type qui caractérise la dispersion observée des moyennes est de 123 ppm (ne figure pas au tableau 3). Le rapport des deux
123 2
0,05 et pour les nombres de degrés de
dispersions : - = 22 est supérieur au seuil donné par la table de Snedecor au risque a =
i 26 1
liberté appropriés.
3.2.4 On peut donc affirmer, au risque les résultats son t différents d’un laboratoire à eu égard à la
choisi de se tromper,
que
dispersion expérimen tale : il y a un effet laboratoire. Cet effet est caractérisé dans le tableau 3 par sb, tel que
S2
% = ‘ibservé entre moyennes - w
5
résultats ultérieurement par un écart-type écart-type de
Une moyenne de n obtenue par un seul laboratoire sera caractérisée St(,) (dit
reproductibilité) tel que :
S2
=s;+w
S2
?n)
n
Si, comme c’est assez souvent le t à rien de faire plusieurs répé-
cas, Sb est relativement grand par rapport à S,, il ne sert pratiquemen
titions dans le but d’améliorer la précision. De toute facon, St ne peut jamais être inf érieur à sb.
NOTE - 11 y a lieu de remarquer que ce qui a été appelé S~bse,.,,6 entre moyennes n’est autre que s2 f( ) quand n = 5.
n
1) Table de Snedecor.
2) En toute rigueur, il faut appliquer un test préliminaire d’homogénéité des dispersions à l’intérieur des laboratoires.
6
---------------------- Page: 6 ----------------------
ISO/TR 7242-1981 (F)
3.2.5 Dans le cas où le test statistique n’a pas permis d’affirmer que la dispersion observée des moyennes est significativement supé-
rieure à la dispersion expérimentale, on ne peut pas calculer d’effet laboratoire, et la dispersion qui affectera un résultat ultérieur sera
établie à partir de S, qui n’est pas significativement différent de S,.
On considère en fait que tous les résultats individuels font partie d’une seule et même populatio n dont persi on n’est due qu’à
bre de répétitions.
l’erreur expérimentale. Cette dispersion va alors dimin uer en fonction du nom
33 . Intervalles de confiance des résultats
On aboutit donc à deux limites de confiance, suivant qu’il existe ou non un effet de laboratoire.
Pour un seuil de probabilité a choisi, on considérera les cas suivants.
3.3.1 Cas où il n’y a pas d’effet laboratoire
1) du tablea u3 représente l’intervalle de confiance affectant un seul résu ltat obtenu par u n laboratoire (St n ‘est pas signi-
St [t
a, (N - ld
ficativement différent de ni de S,,,,. Ce sont trois estimations différentes de la même dispersion) . Cet intervalle diminue comme Ilfi
srl
dans le cas de n répétitions. Dans l’exemple, cette limite n’est pas utilisable puisque l’effet laboratoire existe.
Cas où un effet laboratoire a été mis en évidence
3.3.2
St [ta, (k _I)l du tableau 3 représente l’intervalle de confiance affectant un seul résultat obtenu par un laboratoire; cet intervalle dimi-
nuera dans le cas de n répétitions, suivant la formule :
S2
=s;+L
S2
t
n
Dans l’exemple, cet intervalle est pratiquement indépendant de n puisque Sb (effet laboratoire) est grand devant S,.
Dans les formules précédentes,
est la variable Student-Fischer;
ta
k -1 est le nombre de degrés de liberté de St lorsque Sb est significatif.
34 . II existe une méthode normalisée pour calculer tous les paramètres mentionnés et utilisés dans le tableau 3. Cette méthode est
assez laborieuse et requiert une certaine h
...
Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.