ASTM D5881-95(2005)

NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation:D5881 −95(Reapproved 2005)
Standard Test Method for
(Analytical Procedure) Determining Transmissivity of
Confined Nonleaky Aquifers by Critically Damped Well
Response to Instantaneous Change in Head (Slug)
This standard is issued under the fixed designation D5881; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope 2. Referenced Documents
1.1 This test method covers determination of transmissivity
2.1 ASTM Standards:
from the measurement of water-level response to a sudden
D653Terminology Relating to Soil, Rock, and Contained
changeofwaterlevelinawell-aquifersystemcharacterizedas
Fluids
being critically damped or in the transition range from under-
D4043Guide for Selection of Aquifer Test Method in
damped to overdamped. Underdamped response is character-
Determining Hydraulic Properties by Well Techniques
ized by oscillatory changes in water level; overdamped re-
D4044Test Method for (Field Procedure) for Instantaneous
sponseischaracterizedbyreturnofthewaterleveltotheinitial
Change in Head (Slug) Tests for Determining Hydraulic
static level in an approximately exponential manner. Over-
Properties of Aquifers
damped response is covered in Guide D4043; underdamped
D4750Test Method for Determining Subsurface Liquid
response is covered in D5785, D4043.
Levels in a Borehole or Monitoring Well (Observation
Well) (Withdrawn 2010)
1.2 The analytical procedure in this test method is used in
D5785Test Method for (Analytical Procedure) for Deter-
conjunction with Guide D4043 and the field procedure in Test
mining Transmissivity of Confined NonleakyAquifers by
Method D4044 for collection of test data.
Underdamped Well Response to Instantaneous Change in
1.3 Limitations—Slug tests are considered to provide an
Head (Slug Test)
estimate of the transmissivity of an aquifer near the well
screen. The method is applicable for systems in which the
3. Terminology
dampingparameter, ζ,iswithintherangefrom0.2through5.0.
3.1 Definitions:
The assumptions of the method prescribe a fully penetrating
3.1.1 aquifer, confined—an aquifer bounded above and be-
well (a well open through the full thickness of the aquifer) in
lowbyconfiningbedsandinwhichthestaticheadisabovethe
a confined, nonleaky aquifer.
top of the aquifer.
1.4 The values stated in SI units are to be regarded as
3.1.2 confining bed—ahydrogeologicunitoflesspermeable
standard.
material bounding one or more aquifers.
1.5 This standard does not purport to address all of the
safety concerns, if any, associated with its use. It is the 3.1.3 control well—awellbywhichtheheadandflowinthe
aquifer is changed by pumping, injecting, or imposing a
responsibility of the user of this standard to establish appro-
priate safety and health practices and determine the applica- constant change of head.
bility of regulatory limitations prior to use.
1 2
ThistestmethodisunderthejurisdictionofASTMCommitteeD18onSoiland For referenced ASTM standards, visit the ASTM website, www.astm.org, or
Rock and is the direct responsibility of Subcommittee D18.21 on Groundwater and contact ASTM Customer Service at service@astm.org. For Annual Book of ASTM
Vadose Zone Investigations. Standards volume information, refer to the standard’s Document Summary page on
Current edition approved Nov. 1, 2005. Published December 2005. Originally the ASTM website.
approved in 1995. Last previous edition approved in 2000 as D5881–95 (2000). The last approved version of this historical standard is referenced on
DOI: 10.1520/D5881-95R05. www.astm.org.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959. United States
D5881−95 (2005)
−1
3.1.4 critically damped well response—characterized by the 3.2.20 γ—damping constant [T ].
water level responding in a transitional range between under- 3.2.21 τ—wavelength [T].
−1
damped and overdamped following a sudden change in water 3.2.22 ω—angular frequency [T ].
level. 3.2.23 ζ—dimensionless damping factor [nd].
3.1.5 head, static—the height above a standard datum the
4. Summary of Test Method
surface of a column of water can be supported by the static
pressure at a given point.
4.1 This test method describes the analytical procedure for
analyzing data collected during an instantaneous head (slug)
3.1.6 observation well—a well open to all or part of an
test for well and aquifer response at and near critical damping.
aquifer.
Procedures in conducting a slug test are given in Test Method
3.1.7 overdamped well response—characterized by the wa-
D4044. The analytical procedure consists of analyzing the
ter level returning to the static level in an approximately
response of water level in the well following the change in
exponential manner following a sudden change in water level.
water level induced in the well.
(See for comparison underdamped well response.)
4.2 Theory—The equations that govern the response of well
3.1.8 slug—avolumeofwaterorsolidobjectusedtoinduce
to an instantaneous change in head are treated at length by
a sudden change of head in a well.
Kipp (1). Theflowintheaquiferisgovernedbythefollowing
3.1.9 storage coeffıcient—the volume of water an aquifer
equation for cylindrical flow:
releases from or takes into storage per unit surface area of the
S dh 1 d dh
aquifer per unit change in head. For a confined aquifer, the
5 r (1)
S D
T dt r dr dr
storagecoefficientisequaltotheproductofthespecificstorage
and aquifer thickness.
where:
3.1.10 transmissivity—the volume of water at the existing
h = hydraulic head,
kinematic viscosity that will move in a unit time under a unit
T = aquifer transmissivity, and
hydraulic gradient through a unit width of the aquifer. S = storage coefficient.
3.1.11 underdamped well response—response characterized
4.2.1 The initial condition is at t =0 and h = h , and the
o
by the water level oscillating about the static water level
outer boundary condition is as r − and h−h .
o
following a sudden change in water level (See for comparison
4.2.1.1 An equation is given by Kipp (1) for the skin factor,
overdamped-well response).
that is, the effect of aquifer damage during drilling of the well.
However, this factor is not treated by Kipp (1) and is not
3.1.12 For definitions of other terms used in this test
considered in this procedure.
method, see Terminology D653.
4.2.2 The flow rate balance on the well bore relates the
3.2 Symbols and Dimensions:
2 −1
displacementofthewaterlevelinthewellrisertotheflowinto
3.2.1 T—transmissivity [L T ].
the well:
3.2.2 S—storage coefficient [nd].
dw dh
3.2.3 L—static water column length above top of aquifer
πr 52πr T (2)
c s ? r5rs
dt dr
[L].
where:
3.2.4 L —effective length of water column in a well, equal
e
2 2
to L +(r /r )(b/2) [L]. r = radius of the well casing, and
c c s c
w = displacement of the water level in the well from its
3.2.5 L —length of water column within casing [L].
c
initial position.
3.2.6 L —length of water column within well screen [L].
s
4.2.3 The fourth equation describing the system relating h
−2 s
3.2.7 g—acceleration of gravity [LT ].
and w,comesfromamomentumbalanceequationofBirdetal
3.2.8 h—hydraulic head in the aquifer [L].
(2) as referenced in Kipp (1):
3.2.9 h —initial hydraulic head in the aquifer [L]. 0
o
d
2 2 2
πr pvdz5 2pv 1p 2p 2ρgb πr (3)
* ~ !
3.2.10 h —hydraulic head in the well screen [L]. s 2 1 2 s
s dt
2b
3.2.11 r —radius of well casing [L].
c
where:
3.2.12 r —radius of well screen [L].
s
v = velocity in the well screen interval,
3.2.13 t—time [T].
b = aquifer thickness,
p = pressure,
3.2.14 t`—dimensionless time [nd].
ρ = fluid density,
3.2.15 t—dimensionless time [nd].
g = gravitational acceleration, and
3.2.16 w—water level displacement from the initial static
r = well screen radius.
s
level [L].
3.2.17 w —initial water level displacement [L].
o
3.2.18 α—dimensionless storage parameter [nd]. 4
The boldface numbers in parentheses refer to a list of references at the end of
3.2.19 β—dimensionless inertial parameter [nd]. the text.
D5881−95 (2005)
Thenumericalsubscriptsrefertotheplanesdescribedabove
and shown in Fig. 1. Atmospheric pressure is taken as zero.
5. Solution
5.1 Kipp (1) derives the following differential equation to
representfortheresponseofthedisplacementofwaterlevelin
the well:
d w g g
1 w5 /L (4)
S D
2 e
dt L h 2h
~ !
e s o
where:
L = effective water column length, defined as:
e
2 2
L 5L1 r /r b/2 (5)
~ !~ !
e c s
where:
b = aquifer thickness with initial conditions:
at t50, w5w (6)
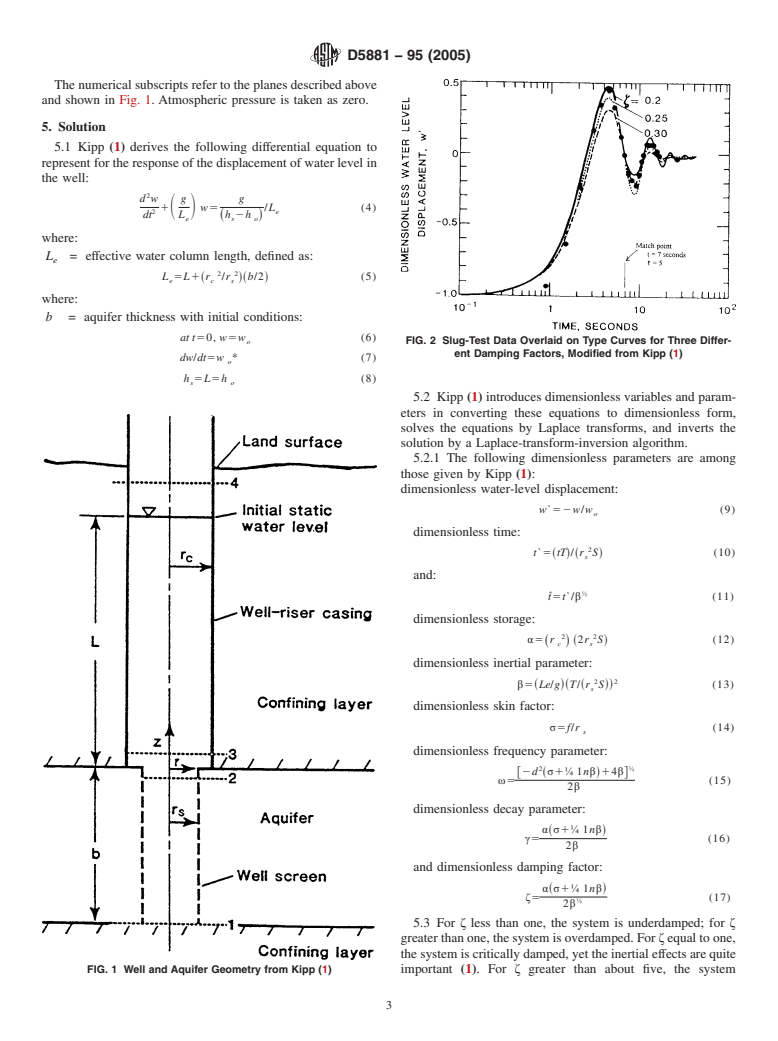
o FIG. 2 Slug-Test Data Overlaid on Type Curves for Three Differ-
ent Damping Factors, Modified from Kipp (1)
dw/dt5w * (7)
o
h 5L5h (8)
s o
5.2 Kipp (1) introduces dimensionless variables and param-
eters in converting these equations to dimensionless form,
solves the equations by Laplace transforms, and inverts the
solution by a Laplace-transform-inversion algorithm.
5.2.1 The following dimensionless parameters are among
those given by Kipp (1):
dimensionless water-level displacement:
w`52w/w (9)
o
dimensionless time:
t`5 tT / r S (10)
~ ! ~ !
s
and:
½
ˆ
t5t`/β (11)
dimensionless storage:
2 2
α5 r ~2r S! (12)
~ !
c s
dimensionless inertial parameter:
2 2
β5~Le/g!~T/~r S!! (13)
s
dimensionless skin factor:
σ5f/r (14)
s
dimensionless frequency parameter:
2 ½
2d σ1¼ 1nβ 14β
@ ~ ! #
ω5 (15)
2β
dimensionless decay parameter:
α σ1¼ 1nβ
~ !
γ5 (16)
2β
and dimensionless damping factor:
α σ1¼ 1nβ
~ !
ζ5 (17)
½
2β
5.3 For ζ less than one, the system is underdamped; for ζ
greaterthanone,thesystemisoverdamped.For ζequaltoone,
thesystemiscriticallydamped,yettheinertialeffectsarequite
FIG. 1 Well andAquifer Geometry from Kipp (1) important (1). For ζ greater than about five, the system
D5881−95 (2005)
TABLE 1 Values of the Dimensionless Water Level Displacement,
responds as if the inertial effects can be neglected and the
w*, Versus Dimensionless Time, t, for Construction of Type
solution of Cooper et al (3) (given in Guide D4043)is
Curves, ζ=0.1 and α=9988.1
applicable. For ζ about 0.2 or less, the approximate solution of
tw8 tw8
vander Kamp (4) is valid (given in Test Method D5785). The
3.162278E−02 −9.994887E−01 3.162278E + 00 7.100277E−01
solution of Kipp (1), the subject of this test method, is
3.636619E−02 −9.993281E−01 3.636619E + 00 6.204110E−01
applicable for the transition zone between systems that are
3.952847E−02 −9.992086E−01 3.952847E + 00 4.871206E−01
4.269075E−02 −9.990793E−01 4.269075E + 00 3.138511E−01
underdamped and overdamped. Solutions are given here for ζ
4.743416E−02 −9.988666E−01 4.743416E + 00 2.218683E−02
ranging from 0.2 to 5.0.
5.375872E−02 −9.985483E−01 5.375872E + 00 −3.226809E−01
6.324555E−02 −9.979965E−01 6.324555E + 00 −5.191564E−01
7.115125E−02 −9.974688E−01 7.115125E + 00 −3.413663E−01
6. Significance and Use
7.905694E−02 −9.968794E−01 7.905694E + 00 3.445623E−05
8.696264E−02 −9.962284E−01 8.696264E + 00 2.889492E−01
6.1 The assumptions of the physical system are given as
9.486833E−02 −9.955161E−01 9.486833E + 00 3.712172E−01
follows:
1.106797E−01 −9.939077E−01 1.106797E + 01 −1.758246E−02
6.1.1 Theaquiferisofuniformthickness,withimpermeable
1.264911E−01 −9.920552E−01 1.264911E + 01 −2.697976E−01
1.423025E−01 −9.899599E−01 1.423025E + 01 2.109260E−02
upper and lower confining boundaries.
1.581139E−01 −9.876230E−01 1.581139E + 01 1.919487E−01
6.1.2 The aquifer is of constant homogeneous porosity and
1.739253E−01 −9.850456E−01 1.739253E + 01 −2.455328E−02
matrix compressibility and constant homogeneous and isotro-
1.897367E−01 −9.822293E−01 1.897367E + 00 −1.392019E−01
2.213594E−01 −9.758851E−01 2.213594E + 01 9.826209E−02
pic hydraulic conductivity.
2.529822E−01 −9.686026E−01 2.529822E + 01 −7.129166E−02
6.1.3 The origin of the cylindrical coordinate system is
2.846050E−01 −9.603946E−01 2.846050E + 01 4.976069E−02
taken to be on the well-bore axis at the top of the aquifer.
3.162278E−01 −9.512748E−01 3.162278E + 01 −3.626029E−02
3.636619E−01 −9.359183E−01 3.636619E + 01 −9.997386E−03
6.1.4 The aquifer is fully screened.
3.952847E−01 −9.259452E−01 3.952847E + 01 7.200932E−03
6.1.5 The well is 100% efficient, that is, the skin factor, f,
4.269075E−01 −9.084819E−01 4.743416E + 01 5.892951E−03
and dimensionless skin factor, σ, are zero. 4.743416E−01 −8.947298E−01 5.375872E + 01 2.737128E−03
5.375872E−01 −8.632514E−01 6.324555E + 01 −1.254582E−03
6.2 The assumptions made in defining the momentum bal-
6.324555E−01 −8.135785E−01 7.115125E + 01 2.961127E−04
7.115125E−01 −7.673017E−01 7.905694E + 01 −5.757717E−05
ance are as follows:
7.905694E−01 −7.169702E−01 8.696264E + 01 −2.991356E−04
6.2.1 The average water velocity in the well is approxi-
8.696264E−01 −6.629659E−01 9.486833E + 01 −1.835296E−04
mately constant over the well-bore section.
9.486833E−01 −6.056883E−01 1.106797E + 02 −1.426791E−04
1.106797E + 00 −4.829810E−01 1.264911E + 02 −1.249977E−04
6.2.2 Frictional head losses from flow in the well are
1.264911E + 00 −3.522848E−01 1.423025E + 02 −1.115579E−04
negligible.
1.423025E + 00 −2.171309E−01 1.581139E + 02 −1.001696E−04
6.2.3 Flow through the well screen is uniformly distributed 1.581139E + 00 −8.105198E−02 1.739253E + 02 −9.109389E−05
1.739253E + 00 5.974766E−02 1.897367E + 02 −8.347056E−05
over the entire aquifer thickness.
1.897367E + 00 1.802728E−01 2.213594E + 02 −7.152232E−05
6.2.4 Change in momentum from the water velocity chang-
2.213594E + 00 4.066508E−01 2.529822E + 02 −6.256450E−05
ing from radial flow through the screen to vertical flow in the 2.529822E + 00 5.647406E−01 2.846050E + 02 −5.560200E−05
2.846050E + 00 6.811030E−01 . .
well are negligible.
7. Procedure
8.5 Calculate the effective static water column length, L ,
7.1 The overall procedure consists of conducting the slug e
from the following:
test field procedure (see Test Method D4044) and analysis of
the field data using this test method.
t
ˆ
t5 (18)
1/2
L /g
~ !
e
NOTE 1—The initial displacement of water level should not exceed 0.1
or 0.2 of the static water column in the well, the measurement of
ˆ
L 5~t/t! g (19)
e
displacement should be within 1% of the initial water-level displacement
and the water-level displacement needs to be calculated independently. Theeffectivestaticwatercolumnlengthshouldagree,within
20%, with the effective length calculated from the system
8. Calculation and Interpretation of Results
geometry, (Eq 5).
8.1 Plotthenormalizedwater-leveldisplacementinthewell 8.6 Calculate the dimensionless inertial parameter, β, itera-
versus t
...