ASTM C1239-06a
(Practice)Standard Practice for Reporting Uniaxial Strength Data and Estimating Weibull Distribution Parameters for Advanced Ceramics
Standard Practice for Reporting Uniaxial Strength Data and Estimating Weibull Distribution Parameters for Advanced Ceramics
SCOPE
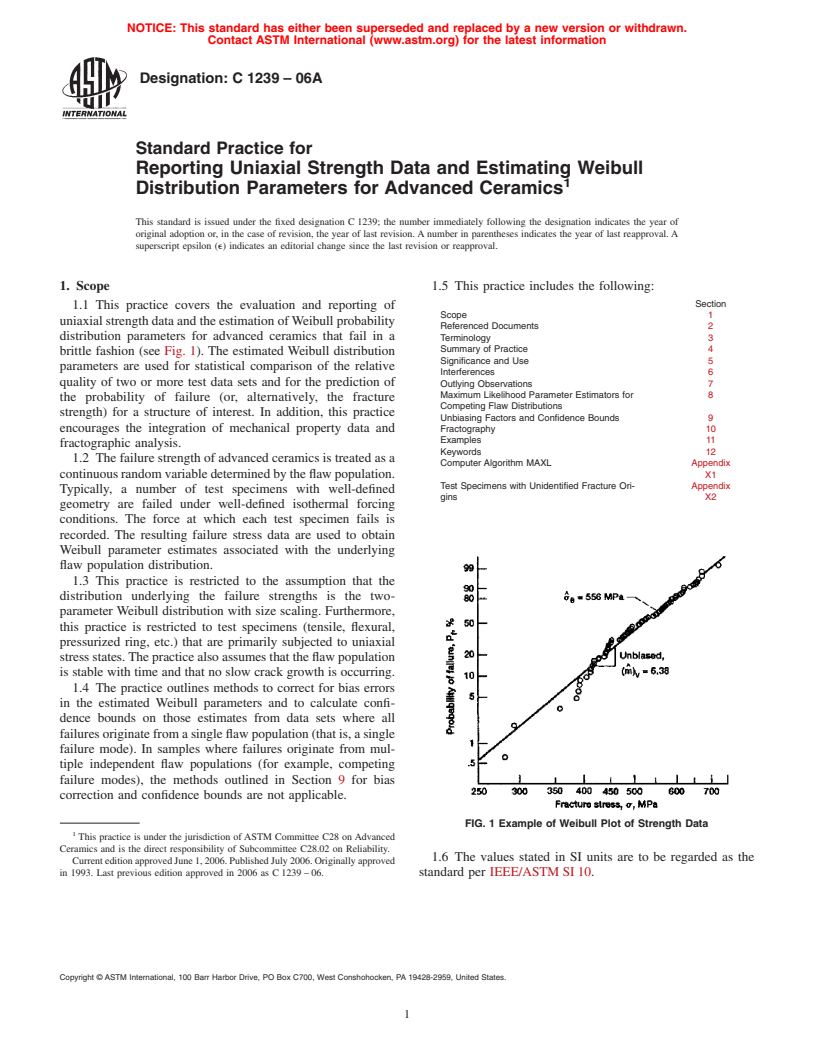
1.1 This practice covers the evaluation and reporting of uniaxial strength data and the estimation of Weibull probability distribution parameters for advanced ceramics that fail in a brittle fashion (see ). The estimated Weibull distribution parameters are used for statistical comparison of the relative quality of two or more test data sets and for the prediction of the probability of failure (or, alternatively, the fracture strength) for a structure of interest. In addition, this practice encourages the integration of mechanical property data and fractographic analysis.
1.2 The failure strength of advanced ceramics is treated as a continuous random variable determined by the flaw population. Typically, a number of test specimens with well-defined geometry are failed under well-defined isothermal forcing conditions. The force at which each test specimen fails is recorded. The resulting failure stress data are used to obtain Weibull parameter estimates associated with the underlying flaw population distribution.
1.3 This practice is restricted to the assumption that the distribution underlying the failure strengths is the two-parameter Weibull distribution with size scaling. Furthermore, this practice is restricted to test specimens (tensile, flexural, pressurized ring, etc.) that are primarily subjected to uniaxial stress states. The practice also assumes that the flaw population is stable with time and that no slow crack growth is occurring.
1.4 The practice outlines methods to correct for bias errors in the estimated Weibull parameters and to calculate confidence bounds on those estimates from data sets where all failures originate from a single flaw population (that is, a single failure mode). In samples where failures originate from multiple independent flaw populations (for example, competing failure modes), the methods outlined in Section for bias correction and confidence bounds are not applicable.
1.5 This practice includes the following:
1.6 The values stated in SI units are to be regarded as the standard per IEEE/ASTM SI 10.
General Information
Relations
Standards Content (Sample)
NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: C 1239 – 06A
Standard Practice for
Reporting Uniaxial Strength Data and Estimating Weibull
1
Distribution Parameters for Advanced Ceramics
This standard is issued under the fixed designation C1239; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (e) indicates an editorial change since the last revision or reapproval.
1. Scope 1.5 This practice includes the following:
Section
1.1 This practice covers the evaluation and reporting of
Scope 1
uniaxialstrengthdataandtheestimationofWeibullprobability
Referenced Documents 2
distribution parameters for advanced ceramics that fail in a
Terminology 3
Summary of Practice 4
brittle fashion (see Fig. 1). The estimated Weibull distribution
Significance and Use 5
parameters are used for statistical comparison of the relative
Interferences 6
quality of two or more test data sets and for the prediction of Outlying Observations 7
Maximum Likelihood Parameter Estimators for 8
the probability of failure (or, alternatively, the fracture
Competing Flaw Distributions
strength) for a structure of interest. In addition, this practice
Unbiasing Factors and Confidence Bounds 9
encourages the integration of mechanical property data and
Fractography 10
Examples 11
fractographic analysis.
Keywords 12
1.2 Thefailurestrengthofadvancedceramicsistreatedasa
ComputerAlgorithm MAXL Appendix
continuousrandomvariabledeterminedbytheflawpopulation. X1
Test Specimens with Unidentified Fracture Ori- Appendix
Typically, a number of test specimens with well-defined
gins X2
geometry are failed under well-defined isothermal forcing
conditions. The force at which each test specimen fails is
recorded. The resulting failure stress data are used to obtain
Weibull parameter estimates associated with the underlying
flaw population distribution.
1.3 This practice is restricted to the assumption that the
distribution underlying the failure strengths is the two-
parameter Weibull distribution with size scaling. Furthermore,
this practice is restricted to test specimens (tensile, flexural,
pressurized ring, etc.) that are primarily subjected to uniaxial
stressstates.Thepracticealsoassumesthattheflawpopulation
is stable with time and that no slow crack growth is occurring.
1.4 The practice outlines methods to correct for bias errors
in the estimated Weibull parameters and to calculate confi-
dence bounds on those estimates from data sets where all
failuresoriginatefromasingleflawpopulation(thatis,asingle
failure mode). In samples where failures originate from mul-
tiple independent flaw populations (for example, competing
failure modes), the methods outlined in Section 9 for bias
correction and confidence bounds are not applicable.
FIG. 1 Example of Weibull Plot of Strength Data
1
This practice is under the jurisdiction ofASTM Committee C28 onAdvanced
Ceramics and is the direct responsibility of Subcommittee C28.02 on Reliability.
1.6 The values stated in SI units are to be regarded as the
CurrenteditionapprovedJune1,2006.PublishedJuly2006.Originallyapproved
in 1993. Last previous edition approved in 2006 as C1239–06. standard per IEEE/ASTMSI10.
Copyright ©ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA19428-2959, United States.
1
---------------------- Page: 1 ----------------------
C 1239 – 06A
2. Referenced Documents exclusive. A simple example is where every test specimen
2
containstheflawdistribution A,whilesomefractionofthetest
2.1 ASTM Standards:
specimensalsocontainsasecondindependentflawdistribution
C1145 Terminology of Advanced Ceramics
B.
C1322 Practice for Fractography and Characterization of
3.2.3 concurrent flaw distributions—type of multiple flaw
Fracture Origins in Advanced Ceramics
distribution in a homogeneous material where every test
E6 Terminology Relating to Methods of Mechanical Test-
specimen of that material contains representative flaws from
ing
each independent flaw population. Within a given test speci-
E178 Practice for Dealing With Outlying Observations
men,allflawpopulationsarethenpresentconcurrentlyandare
E456 Terminology Relating to Quality and Statistics
competing with each other to cause failure. This term is
IEEE/ASTMSI10 American National Standard for Use of
synonymous with “competing flaw distributions.”
the International System of Units (SI): The Modern Metric
3.2.4 effective gage section—that portion of the test speci-
System
men geometry that has been included within the limits of
3. Terminology
integration (volume, area, or edge length) of the Weibull
3.1 Proper use of the following terms and equations will distribution function. In tensile test specimens, the integration
may be restricted to the uniformly stress
...







Questions, Comments and Discussion
Ask us and Technical Secretary will try to provide an answer. You can facilitate discussion about the standard in here.