ASTM D7366-08

NOTICE: This standard has either been superseded and replaced by a new version or withdrawn.
Contact ASTM International (www.astm.org) for the latest information
Designation: D7366 − 08
StandardPractice for
Estimation of Measurement Uncertainty for Data from
Regression-based Methods
This standard is issued under the fixed designation D7366; the number immediately following the designation indicates the year of
original adoption or, in the case of revision, the year of last revision.Anumber in parentheses indicates the year of last reapproval.A
superscript epsilon (´) indicates an editorial change since the last revision or reapproval.
1. Scope 1.5 Associated with the measurement uncertainty is a user-
chosen level of statistical confidence.
1.1 This practice establishes a standard for computing the
measurement uncertainty for applicable test methods in Com- 1.6 Atanyconcentrationintheworkingrange,themeasure-
mittee D19 on Water. The practice does not provide a single- ment uncertainty is plus-or-minus the half-width of the predic-
point estimate for the entire working range, but rather relates tion interval associated with the regression line.
the uncertainty to concentration. The statistical technique of
1.7 It is assumed that the user has access to a statistical
regression is employed during data analysis.
software package for performing regression. A statistician
1.2 Applicable test methods are those whose results come should be consulted if assistance is needed in selecting such a
from regression-based methods and whose data are intra- program.
laboratory (not inter-laboratory data, such as result from
1.8 A statistician also should be consulted if data transfor-
round-robinstudies).Foreachanalysisconductedusingsucha
mations are being considered.
method, it is assumed that a fixed, reproducible amount of
1.9 This standard does not purport to address all of the
sample is introduced.
safety concerns, if any, associated with its use. It is the
1.3 Calculationofthemeasurementuncertaintyinvolvesthe
responsibility of the user of this standard to establish appro-
analysis of data collected to help characterize the analytical
priate safety and health practices and determine the applica-
method over an appropriate concentration range. Example
bility of regulatory limitations prior to use.
sources of data include: 1) calibration studies (which may or
may not be conducted in pure solvent), 2) recovery studies
2. Referenced Documents
(which typically are conducted in matrix and include all 2
2.1 ASTM Standards:
sample-preparation steps), and 3) collections of data obtained
D1129Terminology Relating to Water
as part of the method’s ongoing Quality Control program. Use
of multiple instruments, multiple operators, or both, and
3. Terminology
field-sampling protocols may or may not be reflected in the
3.1 Definitions of Terms Specific to This Standard:
data.
3.1.1 confidence level—the probability that the prediction
1.4 In any designed study whose data are to be used to
interval from a regression estimate will encompass the true
calculate method uncertainty, the user should think carefully
value of the amount or concentration of the analyte in a
about what the study is trying to accomplish and much
subsequent measurement. Typical choices for the confidence
variation should be incorporated into the study. General guid-
level are 99% and 95%.
ance on designing studies (for example, calibration, recovery)
3.1.2 fitting technique—a method for estimating the param-
is given in Appendix A. Detailed guidelines on sources of
eters of a mathematical model. For example, ordinary least
variation are outside the scope of this practice, but general
squares is a fitting technique that may be used to estimate the
points to consider are included in Appendix B, which is not
parameters a,a,a , … of the polynomial modely=a +a x
0 1 2 0 1
intended to be exhaustive. With any study, the user must think
+a x + …, based on observed {x,y} pairs. Weighted least
carefully about the factors involved with conducting the
squares is also a fitting technique.
analysis, and must realize that the computed measurement
3.1.3 lack-of-fit (LOF) test—a statistical technique when
uncertainty will reflect the quality of the input data.
replicate data are available; computes the significance of
This practice is under the jurisdiction ofASTM Committee D19 on Water and
is the direct responsibility of Subcommittee D19.02 on Quality Systems, For referenced ASTM standards, visit the ASTM website, www.astm.org, or
Specification, and Statistics. contact ASTM Customer Service at service@astm.org. For Annual Book of ASTM
Current edition approved Aug. 1, 2008. Published September 2008. DOI: Standards volume information, refer to the standard’s Document Summary page on
10.1520/D7366-08. the ASTM website.
Copyright © ASTM International, 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959. United States
D7366 − 08
residual means to replicate y variability, to indicate whether 4.1.2 The total number of data points in any designed study
deviations from model predictions are reasonably accounted should be kept high. Blanks may or may not be included,
for by random variability, thus indicating that the model is depending on the data-quality objectives of the test method.
adequate; at each concentration, compares the amount of 4.1.3 In applying regression to any applicable data set, the
residual variation from model prediction with the amount of proper fitting technique (for example, ordinary least squares
residual variation from the observed mean. (OLS) or weighted least squares (WLS)) must be determined
(for fitting the proposed model to the data).
3.1.4 least squares—fitting technique that minimizes the
4.1.4 Theresidualpatternandthelack-of-fittestareusedto
sum of squared residuals between observed y values and those
evaluate the adequacy of the chosen model.
predicted by the model.
4.1.5 The magnitude of the half-width of the prediction
3.1.5 model—mathematical expression (for example,
interval must be evaluated, remembering that accepting or
straight line, quadratic) relating y (directly measured value) to
rejecting the amount of uncertainty is a judgment call, not a
x (concentration or amount of analyte).
statistical decision.
3.1.6 ordinary least squares (OLS)—leastsquares,whereall
5. Significance and Use
data points are given equal weight.
5.1 Appropriate application of this practice should result in
3.1.7 prediction interval—a pair of prediction limits (an
an estimate of the test-method’s uncertainty (at any concentra-
“upper”and“lower”)usedtobracketthe“next”observationat
tion within the working range), which can be compared with
a certain level of confidence.
data-quality objectives to see if the uncertainty is acceptable.
3.1.8 p-value—the statistical significance of a test; the
5.2 With data sets that compare recovered concentration
probability value associated with a statistical test, representing
withtrueconcentration,theresultingregressionplotallowsthe
the likelihood that a test statistic would assume or exceed a
correction of the recovery data to true values. Reporting of
certainvaluepurelybychance,assumingthenullhypothesisis
such corrections is at the discretion of the user.
true(alowp-valueindicatesstatisticalsignificanceatalevelof
5.3 This practice should be used to estimate the measure-
confidence equal to 1.0 minus the p-value).
ment uncertainty for any application of a test method where
3.1.9 regression—an analysis technique for fitting a model
measurement uncertainty is important to data use.
to data; often used as a synonym for OLS.
6. Procedure
3.1.10 residual—error in the fit between observed and
6.1 Introduction
modeled concentration; response minus fit.
6.1.1 For purposes of this practice, only regression-based
3.1.11 root mean square error (RMSE)—an estimate of the
methods are applicable. An example of a module that is not
measurement standard deviation (that is, inherent variation in
regression-based is a balance. If an object is placed on a
the measurement system).
balance, the readout is in the desired units; that is, in units of
3.1.12 significance level—the likelihood that a measured or
mass. No user intervention is required to get to the needed
observed result came about due to simple random behavior. result. However, for an instrument such as a chromatograph or
a spectrometer, the raw data (for example, peak area or
3.1.13 uncertainty (of a measurement)—the lack of exact-
absorbance) must be transformed into meaningful units, typi-
ness in measurement (for example, due to sampling error,
cally concentration. Regression is at the core of this transfor-
measurement variation, and model inexactness); a statistical
mation process.
interval within which the measurement error is believed to
6.1.2 One additional distinction will be made regarding the
occur, at some level of confidence.
applicability of this protocol. This practice will deal only with
3.1.14 weight—coefficient assigned to observations in order
intralaboratory data. In other words, the variability introduced
to manipulate their relative influence in subsequent calcula-
by collecting results from more than one lab is not being
tions. For example, in weighted least squares, noisy observa-
considered. The examples that are shown here are for one
tionsareweighteddownwards,whileprecisedataareweighted
method with one operator. If the user wishes, additional
upwards.
operators may be included in the design, to capture multiple-
operator variability.
3.1.15 weighted least squares (WLS)—least squares, where
6.1.3 Abrief example will help illustrate the importance of
data points are weighted inversely proportional to their vari-
estimating measurement uncertainty. A sample is to be ana-
ance (“noisiness”).
lyzedtodetermineifitisundertheupperspecificationlimitof
5(theactualunitsofconcentrationdonotmatter).Thefinaltest
4. Summary of Practice
result is 4.5. The question then is whether the sample should
4.1 Key points of the statistical protocol for measurement
pass or fail. Clearly, 4.5 is less than 5. If the numbers are
uncertainty are:
treated as being absolute, then the sample will pass. However,
4.1.1 Withintheworkingrangeofthemethod’sdataset,the such a judgment call ignores the variability that always exists
estimate of the method uncertainty at any given concentration with a measurement. The width of any measurement’s uncer-
is calculated to be plus-or-minus the half-width of the predic- tainty interval depends not only on the noisiness of the data,
tion interval. butalsoontheconfidenceleveltheuserwishestoassume.This
D7366 − 08
latter consideration is not a statistical decision, but a reasoned However, the preferred formula comes from modeling the
decision that must be based on the needs of the customer, the standard deviation. In other words, the actual standard-
intendeduseofthedata,orboth.Oncetheconfidencelevelhas deviation values are plotted versus true concentration; an
been chosen, the interval can be calculated from the data. In appropriate model is then fitted to the data. The reciprocal
this example, if the uncertainty is determined to be 61.0, then square of the equation for the line is then used to calculate the
there is serious doubt as to whether the sample passes or not, weights.Thesimplestmodelisastraightline,butmoreprecise
since the true value could be anywhere between 3.5 and 5.5. modeling should be done if the situation requires it. (In
On the other hand, if the uncertainty is only 60.1, then the practice, it is best to normalize the weight formula by dividing
sample could be passed with a high level of comfort. Only by by the sum of all the reciprocal squares. This process assures
making a sound evaluation of the uncertainty can the user that the root mean square error is correct.)
determine how to apply the sample estimate he or she has
6.2.2.3 In sum, two choices, which are independent of each
obtained. The following protocol is designed to answer ques-
other, must be made in performing regression. These two
tions such as: 4.5 6 ?
choices are a model and a fitting technique. In practice, the
optionsforthemodelaretypicallyastraightlineoraquadratic,
6.2 Regression Diagnostics for Recovery Data
while the customary choices for the fitting technique are
6.2.1 Analysts who routinely use chromatographs and spec-
ordinary least squares and weighted least squares.
trometersarefamiliarwiththebasicsoftheregressionprocess.
6.2.2.4 However, a straight line is not automatically associ-
Thefinalresultsare:1)aplotthatvisuallyrelatestheresponses
ated with OLS, nor is a quadratic automatically paired with
(onthey-axis)tothetrueconcentrations(onthex-axis)and2)
WLS. The fitting technique depends solely on the behavior of
an equation that mathematically relates the two variables.
the response standard deviations (that is, do they trend with
6.2.2 Underlying these results are two basic choices: 1) a
concentrations). The model choice is not related to these
model, such as a straight line or some sort of curved line, and
standarddeviations,butdependsprimarilyonwhetherthedata
2) a fitting technique, which is a version of least squares. The
points exhibit some type of curvature.
modeling choices are generally well known to most analysts,
6.2.3 Once an appropriate model and fitting technique have
but the fitting-technique choices are typically less well under-
been chosen, the regression line and plot can be determined.
stood.Thetwomostcommonformsofleast-squaresfittingare
One other very important feature can also be calculated and
discussed next.
graphed. That feature is the prediction interval, which is an
6.2.2.1 Ordinary least squares (OLS) assumes that the
“envelope” around the line itself and which reports the
variance of the responses does not trend with concentration. If
uncertainty (at the chosen confidence level) in a future mea-
thevariancedoestrendwithconcentration,thenweightedleast
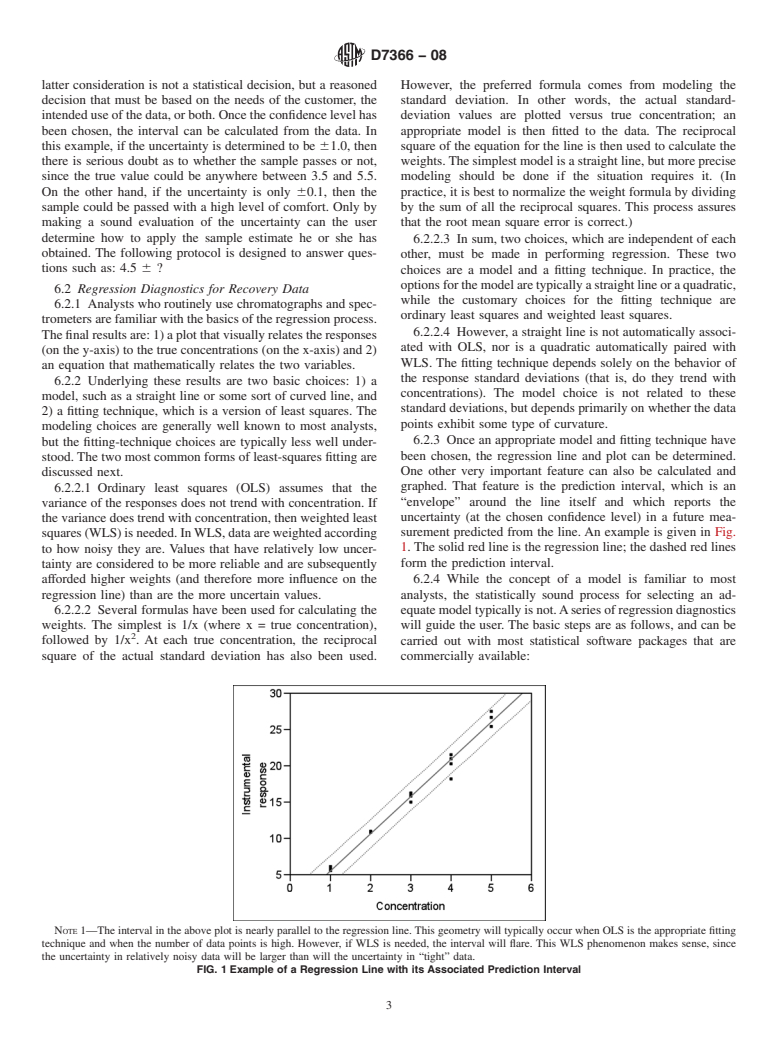
surement predicted from the line.An example is given in Fig.
squares(WLS)isneeded.InWLS,dataareweightedaccording
1.The solid red line is the regression line; the dashed red lines
to how noisy they are. Values that have relatively low uncer-
form the prediction interval.
tainty are considered to be more reliable and are subsequently
afforded higher weights (and therefore more influence on the 6.2.4 While the concept of a model is familiar to most
regression line) than are the more uncertain values. analysts, the statistically sound process for selecting an ad-
6.2.2.2 Several formulas have been used for calculating the
equatemodeltypicallyisnot.Aseriesofregressiondiagnostics
weights. The simplest is 1/x (where x = true concentration), will guide the user. The basic steps are as follows, and can be
followed by 1/x . At each true concentration, the reciprocal carried out with most statistical software packages t
...